van der Waals

A monatomic gas obeys the van der Waals equation

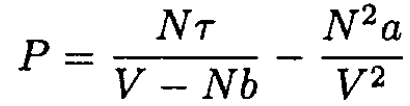
and has a heat capacity C_V = 3N/2 in the limit V → ∞.

a) Prove, using thermodynamic identities and the equation of state, that

b) Use the preceding result to determine the entropy of the van der Waals gas, S(τ, V) to within an additive constant.

c) Calculate the internal energy ε(τ, V) to within an additive constant.

d) What is the final temperature when the gas is adiabatically compressed from (V₁, τ₁) to final volume V₂?

e) How much work is done in this compression?

SOLUTION

a) The heat capacity C_V is defined as

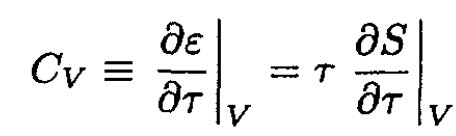(1)

By using the Maxwell relation

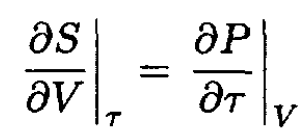(2)

we may write

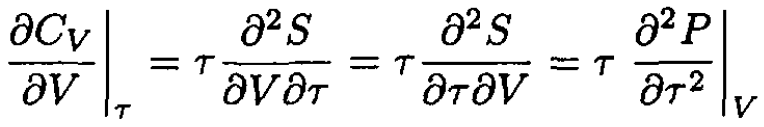(3)

Substituting the van der Waals equation of state

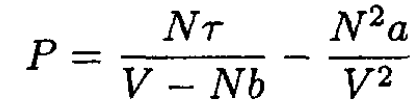(4)

into (3) gives

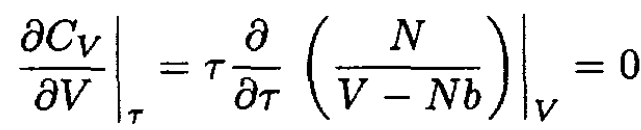(5)

b) The entropy S(τ, V) may be computed from

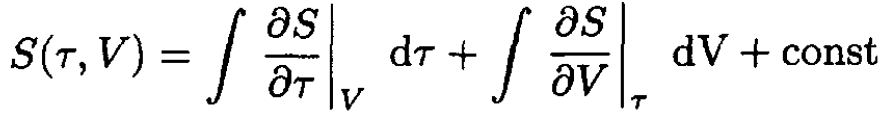(6)

We were given that C_V = 3N/2 at V → ∞, therefore, again using (2) and (S.4.52.4), we obtain

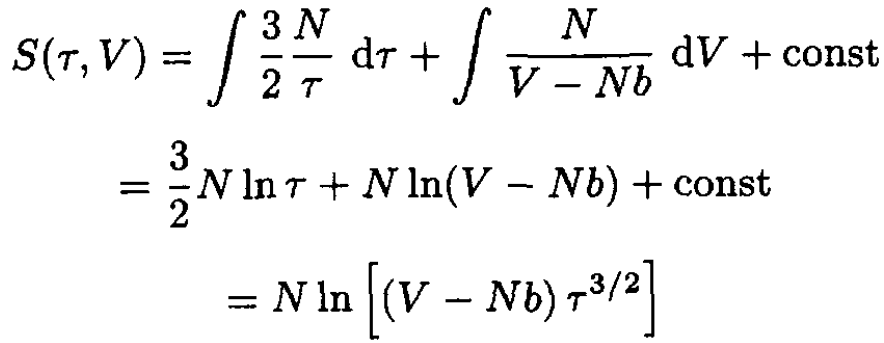(7)

c) The internal energy ε(τ, V) may be calculated in the same way from

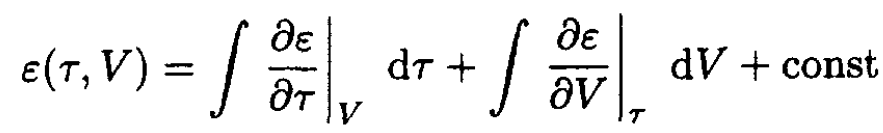(8)

Now, from dε = τ dS – P dV, we have

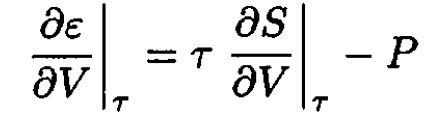(9)

and using (4) and (7), we get

(10)

So, (8) becomes

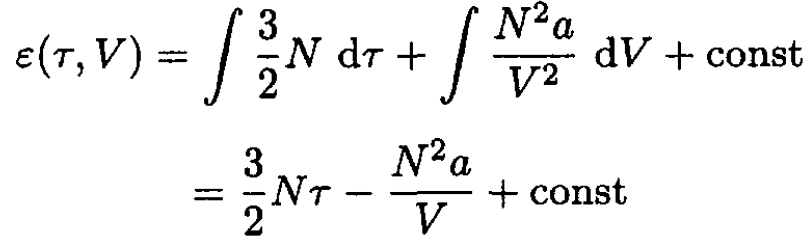(11)

d) During adiabatic compression, the entropy is constant, so from (7)

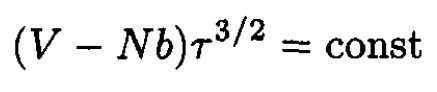(12)

and we have

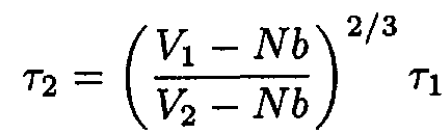(13)

e) The work done is given by the change in internal energy ε since the entropy is constant:

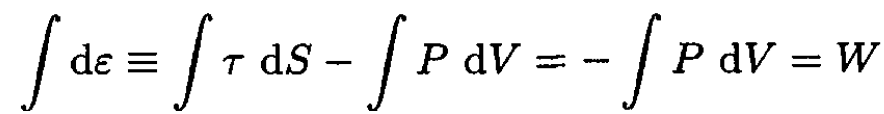(14)

From (11), we arrive at

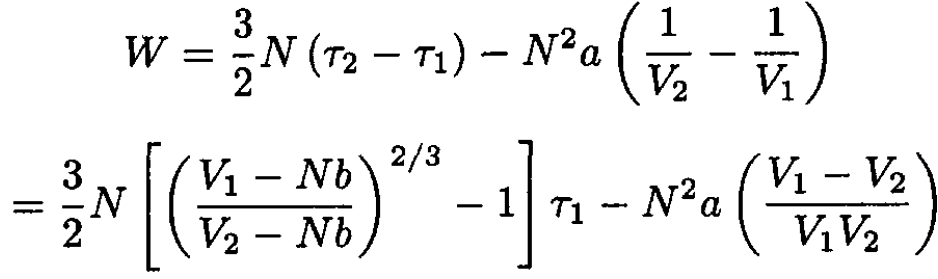(15)