Photon Gas

Consider a photon gas at temperature T inside a container of volume V. Derive the equation of state and compare it to that of the classical ideal gas (which has the equation PV/τ = const). Also compute the energy of the photon gas in terms of PV. You need not get all the numerical factors in this derivation.

SOLUTION

The photon gas is a Bose gas (s = 0) with zero chemical potential (μ = 0), leading to Planck’s distribution:

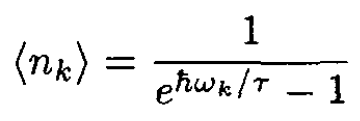(1)

Replacing the sum over different modes by an integral in spherical coordinates, we may write, for the number of quantum states in a volume V,

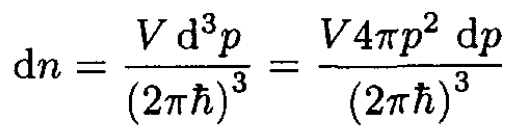(2)

Substituting p = hω /c into (2) and taking into account the two possible transverse polarizations of photons, we obtain

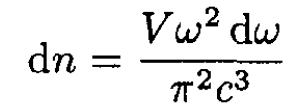(3)

Let us calculate the Helmholtz free energy F. For a Bose gas with μ = 0, the grand thermodynamic potential Ω is given by

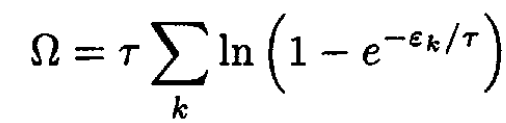(4)

The free energy F would coincide with Ω (since F = Nμ + Ω = Ω). Again replacing the sum by an integral in (4) and substituting ξ = hω/τ yield

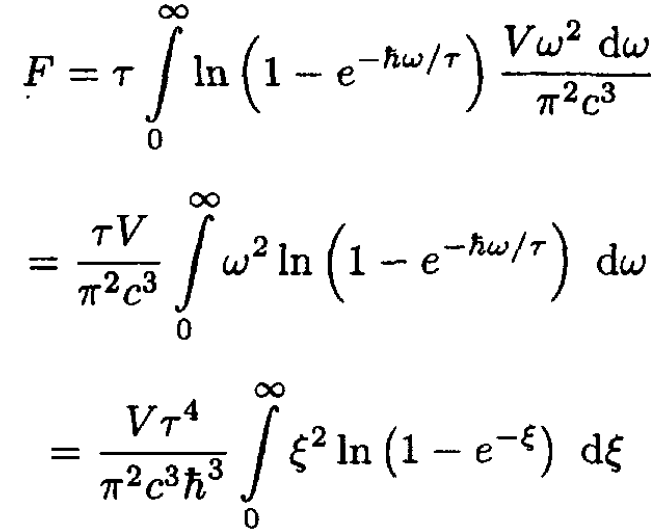(5)

Integrating by parts gives

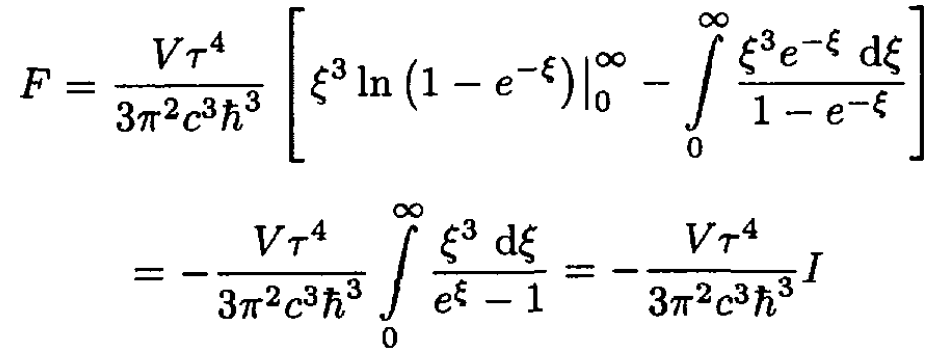(6)

where

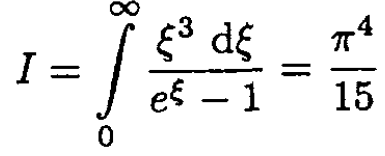
although we really do not need this, and so

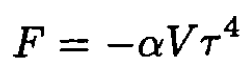
with α a positive constant. The pressure P of the photon gas is

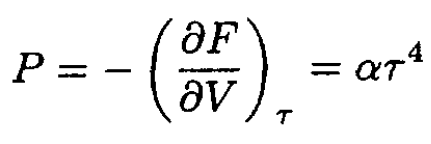(7)

The entropy S of the gas is given by

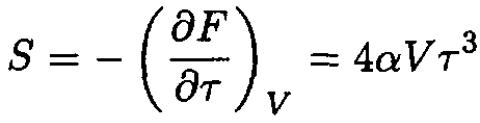(8)

The energy E may now be found from

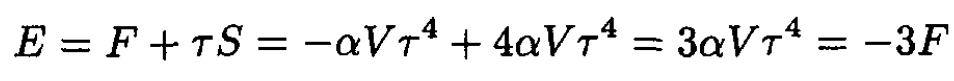(9)

Comparing (7) and (9) gives

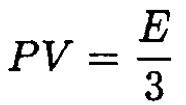(10)

Note that this result is the same as for an ultrarelativistic electron gas (which has the same dispersion law E = pc). The total number of photons is given by

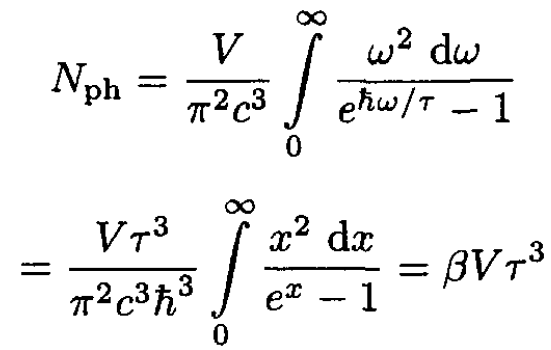(11)

where we let

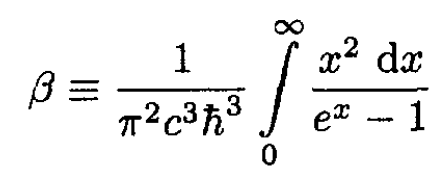
Comparing (9)–( 10) with (11), we can write

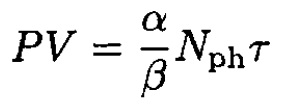(12)

So, similar to the classical ideal gas, we have PV/τ = const.