AdS Space

That AdS space enjoys certain properties which make it a natural candidate for a holographic Hamiltonian description. In this lecture we will describe a very precise version of AdS “Holography” which grew out of the mathematics of string theory. The remarkable precision is due to the unusually high degree of symmetry of the theory which includes a powerful version of supersymmetry. However we will downplay the mathematical aspects of the theory and concentrate on those physical principles which are likely to be general.

The particular space that we will be interested in is not simple 5-dimensional AdS but rather AdS(5)⊗S(5)[7][8][9].This is a 10-dimensional product space consisting of two factors, the 5-dimensional AdS and a 5-sphere S(5). Why the S(5)? The reason involves the high degree of supersymmetry enjoyed by superstring theory. Generally the kind of super gravity theories that emerge from string theory don't have cosmological constants. But by bending some of the directions of space into compact manifolds it becomes possible to generate a cosmological constant for the resulting lower dimensional Kaluza-Klein type theory. From a conceptual point of view the extra internal 5-sphere is not important. From a mathematical point of view it is essential if we want to be able to make precision statements.

We will begin with a brief review of AdS geometry. For our purposes 5-dimensional AdS space may be considered to be a solid 4-dimensional spatial ball times the infinite time axis. The geometry can be described by dimensionless coordinates t, r, Ω where t is time, r is the radial coordinate (0 ≤ r < 1) and Ω parameterizes the unit 3-sphere.The geometry has uniform curvature R−2 where R is the radius of curvature. The metric we will use is

 (1.1)

There is another form of the metric which is in common use,

 (1.2)

where i runs from 1 to 3.

The metric in equation 1.2 is related to 1.1 in two different ways. First of all it is an approximation to equation 1.1 in the vicinity of a point on the boundary at r = 1.The 3-sphere is replaced by the flat tangent plane parameterized by xi and the radial coordinate is replaced by y, with y = (1 − r).

The second way that equations 1.1 and 1.2 are related is that 1.2 is the exact metric of an incomplete patch of AdS space. A time-like geodesic can get to y = ∞ in a finite proper time so that the space in equation 1.2 is not geodesically complete. It has a horizon at y = ∞. When interpreted in this manner, time coordinates appearing in 1.1 and 1.2 are not the same.

The metric 1.2 may be expressed in terms of the coordinate z = 1/y.

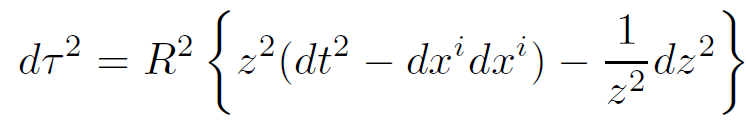 (1.3)

In this form it is clear that there is a horizon at z = 0 since the time–time component of the metric vanishes there. The boundary is at z = ∞. To construct the space AdS(5)⊗S(5) all we have to do is define 5 more coordinates ω₅ describing the unit 5-sphere and add a term to the metric

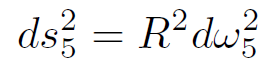 (1.4)

Although the boundary of AdS is an infinite proper distance from any point in the interior of the ball, light can travel to the boundary and back in a finite time. For example, it takes a total amount of (dimensionless) time t = π for light to make a round trip from the origin at r = 0 to the boundary at r = 1 and back. For all practical purposes AdS space behaves like a finite cavity with reflecting walls. The size of the cavity is of order R. In what follows we will think of the cavity size R as being much larger than any microscopic scale such as the Planck or string scale.

_________________________________________________________

Supplement on Properties of AdS metric

1) The point r = 0 is the center of the Anti de Sitter space and r varies from 0 to 1 in the space. A radial null geodesic satisfies (1 + r²)²dt² = 4dr², which means that a light beam will traverse the infinite proper distance in r from 0 to 1 back to 0 in a round trip time given by π, which makes the space causally finite.

2) The metric is singular at r = 1 in all components. A unit coordinate time interval corresponds to increasingly large proper time intervals.

3) Near r = 1, the metric is approximately conformal, which means that light rays move at 45^o angles near the boundary.

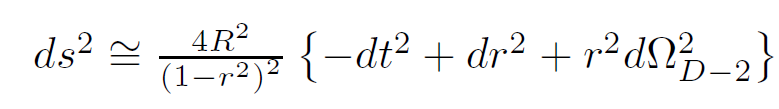
Light rays move slower (by a factor of 2) near the center of the Anti de Sitter space.

4) Generally, the spatial metric is that of a uniformly (negatively) curved space, a hyperbolic plane (or the Poincare disk).