المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
معنى قوله تعالى : وَالشُّعَرَاءُ يَتَّبِعُهُمُ الْغَاوُونَ
2025-04-07
معنى قوله تعالى : وَالطَّيْرُ صَافَّاتٍ كُلٌّ قَدْ عَلِمَ صَلاتَهُ وَتَسْبِيحَهُ
2025-04-07
معنى قوله تعالى : وَالْوَزْنُ يَوْمَئِذٍ الْحَقُّ
2025-04-07
معنى قوله تعالى : وَأَنْ أَقِمْ وَجْهَكَ لِلدِّينِ حَنِيفًا
2025-04-07
معنى قوله تعالى : وَإِنَّ اللَّهَ رَبِّي وَرَبُّكُمْ فَاعْبُدُوهُ
2025-04-07
معنى قوله تعالى : وَإِنْ خِفْتُمْ عَيْلَةً
2025-04-07

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
‏أنماط العلاقات بين الأفراد
27-6-2016
حكم الأسهم الثلاثة التي للإمام
21-11-2015
وتواصوا بالصبر
25-9-2017
أخلاقيات إسلامية رفيعة
25-11-2020
Stressed vowel system FOOT, GOOSE
2024-04-17
Coloring
31-5-2021


اقتران بدائي Antidetevative Function  
  
2861   01:26 صباحاً   التاريخ: 29-10-2015
المؤلف : صالح رشيد بطارسه
الكتاب أو المصدر : معجم الرياضيات
الجزء والصفحة : 35
القسم : الرياضيات / الرياضيات العامة /


أقرأ أيضاً
ذوبان الأس Exponent Solution
التاريخ: 9-11-2015 1762
Descartes and His Coordinate System
التاريخ: 11-1-2016 2431
اقتران ذو متغيرين Two Variables Function
التاريخ: 29-10-2015 1756
تركيب الاقترانات Composition of functions
التاريخ: 3-11-2015 10915

هو الاقتران م(س) الذي مشتقته الأولى الاقتران ق(س) المتصل على الفترة [ أ, ب] ويسمى م(س) حيث ان

أي ان مشتقة الاقتران البدائي هي نفسها الاقتران ق(س) يمكن أن يقال ان الاقتران البدائي م (س) هو نفسه الاقتران المكامل ت (س) ولكن بفارقين فقط .

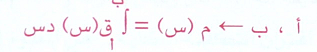
  • حدود تكامل الاقتران البدائي  ثابتين هما :

 

أما حدود تكامل الاقتران البدائي فثابت ومتغير هما :

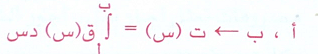
  • أما الاقتران البدائي ليس دائماً متصلاً .

أما الاقتران المكامل فدائماً متصلاً .

 

 

 




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
التاريخ / 2025-04-04

الأخبار العلمية
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
التاريخ / 2025-04-04

الساحة الاسلامية
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
التاريخ / 2025-04-07