Ultrametric

An ultrametric is a metric which satisfies the following strengthened version of the triangle inequality,

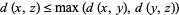for all 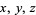. At least two of 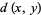, , 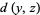and 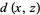 are the same.

Let 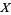 be a set, and let  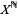(where N is the set of natural numbers) denote the collection of sequences of elements of  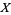(i.e., all the possible sequences 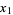, , 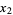, 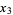...). For sequences 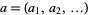, , 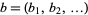let 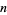 be the number of initial places where the sequences agree, i.e., 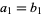, , 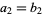..., 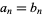, but 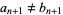. Take  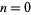if 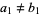. Then defining  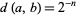gives an ultrametric.

The p-adic norm metric is another example of an ultrametric.