Matrix 1-Inverse
المؤلف:
Campbell, S. L. and Meyer, C. D. Jr.
المصدر:
Generalized Inverses of Linear Transformations. New York: Dover, 1991.
الجزء والصفحة:
...
29-3-2021
1904
Matrix 1-Inverse
An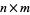 
matrix 
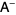is a 1-inverse of an 
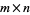matrix 
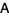for which
 |
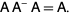(1)
|
The Moore-Penrose matrix inverse is a particular type of 1-inverse.
A matrix equation
 |
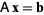(2)
|
has a solution iff
 |
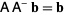(3)
|
(Campbell and Meyer 1991).
Let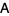 
be an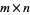 
matrix and use elementary row operations (through premultiplication by a nonsingular matrix 
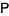obtained by performing the same operations on the identity matrix) and elementary column operations (through postmultiplication by a nonsingular matrix 
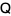obtained by performing the same operations on the identity matrix) to transform 
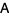into the form
 |
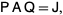(4)
|
where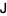 
is the block matrix
![J=[I 0; 0 0]](https://mathworld.wolfram.com/images/equations/Matrix1-Inverse/NumberedEquation5.gif) |
(5)
|
and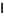 
is an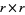 
identity matrix with 
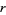the rank of 
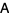. Then a matrix 
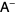is a 1-inverse of 
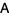iff there are appropriately dimensional matrices 
, 
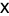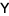and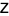 
such that
![A^-=Q[I X; Y Z]P](https://mathworld.wolfram.com/images/equations/Matrix1-Inverse/NumberedEquation6.gif) |
(6)
|
(Jodár et al. 1991).
REFERENCES:
Campbell, S. L. and Meyer, C. D. Jr. Generalized Inverses of Linear Transformations. New York: Dover, 1991.
Jodár, L.; Law, A. G.; Rezazadeh, A.; Watson, J. H.; and Wu, G. "Computations for the Moore-Penrose and Other Generalized Inverses." Congress. Numer. 80, 57-64, 1991.
Rao, C. R. and Mitra, S. K. Generalized Inverse of Matrices and Its Applications. New York: Wiley, 1971.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
