Random Walk--2-Dimensional

In a plane, consider a sum of 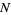 two-dimensional vectors with random orientations. Use phasor notation, and let the phase of each vector be random. Assume  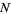unit steps are taken in an arbitrary direction (i.e., with the angle  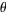uniformly distributed in  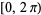and not on a lattice), as illustrated above. The position  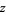in the complex plane after  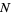steps is then given by

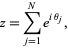(1)

which has absolute square

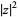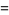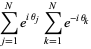			(2)
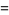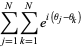			(3)
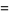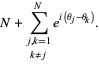			(4)

Therefore,

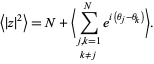(5)

Each unit step is equally likely to be in any direction (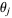 and 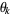). The displacements are random variables with identical means of zero, and their difference is also a random variable. Averaging over this distribution, which has equally likely positive and negative values yields an expectation value of 0, so

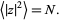(6)

The root-mean-square distance after 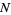 unit steps is therefore

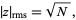(7)

so with a step size of 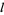, this becomes

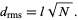(8)

In order to travel a distance ,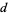

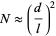(9)

steps are therefore required.

Amazingly, it has been proven that on a two-dimensional lattice, a random walk has unity probability of reaching any point (including the starting point) as the number of steps approaches infinity.

REFERENCES:

McCrea, W. H. and Whipple, F. J. W. "Random Paths in Two and Three Dimensions." Proc. Roy. Soc. Edinburgh 60, 281-298, 1940.