Hofstadter G-Sequence

The sequence defined by 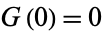 and

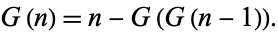(1)

The first few terms for 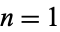, 2, ... are 1, 1, 2, 3, 3, 4, 4, 5, 6, 6, 7, 8, 8, 9, 9, ... (OEIS A005206).

This can be written as a simple recurrence relation

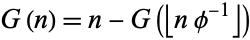(2)

with 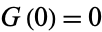 and 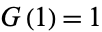 and where  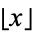is the floor function and  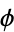the golden ratio.

Closed forms include

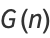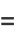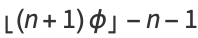			(3)
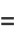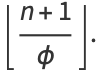			(4)

REFERENCES:

Gault, D. and Clint, M. "'Curiouser and Curiouser,' Said Alice. Further Reflections on an Interesting Recursive Function." Internat. J. Computer Math. 26, 35-43, 1988.

Gould, H. W.; Kim, J. B.; and Hoggatt, V. E. Jr. "Sequences Associated with T-Ary Coding of Fibonacci's Rabbits." Fib. Quart. 15, 311-318, 1977.

Granville, V. and Rasson, J. P. "A Strange Recursive Relation." J. Number Th. 30, 238-241, 1988.

Grytczuk, J. "Another Variation on Conway's Recursive Sequence." Discr. Math. 282, 149-161, 2004.

Hofstadter, D. R. Gödel, Escher, Bach: An Eternal Golden Braid. New York: Vintage Books, p. 137, 1989.

Sloane, N. J. A. Sequence A005206/M0436 in "The On-Line Encyclopedia of Integer Sequences."