


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-6-2020
Date: 6-2-2020
Date: 17-11-2019
|
For any algebraic number  of degree
of degree 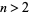 , a rational approximation
, a rational approximation 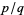 to
to  must satisfy
must satisfy
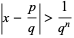 |
for sufficiently large 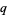 . Writing
. Writing 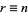 leads to the definition of the irrationality measure of a given number. Apostol (1997) states the theorem in the slightly modified but equivalent form that there exists a positive constant
leads to the definition of the irrationality measure of a given number. Apostol (1997) states the theorem in the slightly modified but equivalent form that there exists a positive constant 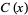 depending only on
depending only on  such that for all integers
such that for all integers 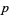 and
and 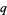 with
with 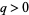 ,
,
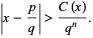 |
REFERENCES:
Apostol, T. M. "Liouville's Approximation Theorem." §7.3 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 146-148, 1997.
Courant, R. and Robbins, H. "Liouville's Theorem and the Construction of Transcendental Numbers." §2.6.2 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 104-107, 1996.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|