


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-1-2020
Date: 11-2-2020
Date: 3-6-2020
|
Levy (1963) noted that
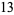 |
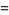 |
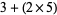 |
(1) |
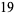 |
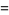 |
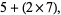 |
(2) |
and from this observation, conjectured that all odd numbers 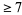 are the sum of a prime plus twice a prime. This conjecture is a stronger version of the weak Goldbach conjecture and has been verified up to
are the sum of a prime plus twice a prime. This conjecture is a stronger version of the weak Goldbach conjecture and has been verified up to 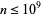 (Corbit 1999).
(Corbit 1999).
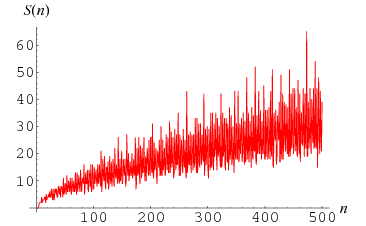
The number of ways 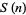 to express
to express 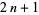 as
as 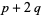 for
for 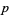 and
and 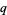 primes and
primes and 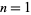 , 2, ... are 0, 0, 0, 1, 2, 2, 2, 2, 4, 2, 3, 3, 3, 4, 4, ... (OEIS A046927).
, 2, ... are 0, 0, 0, 1, 2, 2, 2, 2, 4, 2, 3, 3, 3, 4, 4, ... (OEIS A046927).
REFERENCES:
Corbit, D. "Conjecture on Odd Numbers." sci.math posting. Nov 19, 1999. https://groups-beta.google.com/group/sci.math/msg/539c96e47e3ed582?hl=en&.
Hodges, L. "A Lesser-Known Goldbach Conjecture." Math. Mag. 66, 45-47, 1993.
Levy, H. "On Goldbach's Conjecture." Math. Gaz. 47, 274, 1963.
Sloane, N. J. A. Sequence A046927 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
الحوزة العلمية تؤكد أنّ مهرجان تعزيز الذاكرة يهدف إلى التعريف بالماضي واستلهام الدروس والعبر
|
|
|