


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-10-2020
Date: 24-10-2019
Date: 18-10-2020
|
The word "convergent" has a number of different meanings in mathematics.
Most commonly, it is an adjective used to describe a convergent sequence or convergent series, where it essentially means that the respective series or sequence approaches some limit (D'Angelo and West 2000, p. 259).
The rational number obtained by keeping only a limited number of terms in a continued fraction is also called a convergent. For example, in the simple continued fraction for the golden ratio,
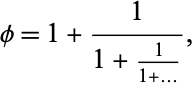 |
(1) |
the convergents are
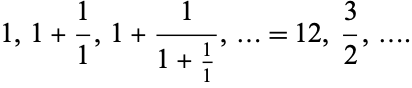 |
(2) |
Convergents are commonly denoted 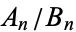 ,
, 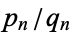 ,
, 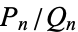 (ratios of integers), or
(ratios of integers), or 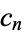 (a rational number).
(a rational number).
Given a simple continued fraction ![[b_0;b_1,b_2,...]](https://mathworld.wolfram.com/images/equations/Convergent/Inline5.gif) , the
, the 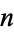 th convergent is given by the following ratio of tridiagonal matrix determinants:
th convergent is given by the following ratio of tridiagonal matrix determinants:
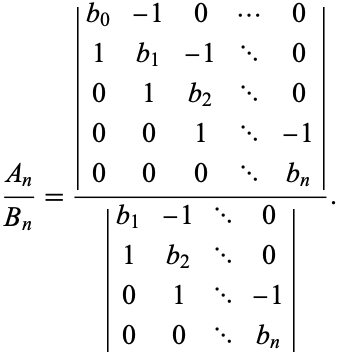 |
(3) |
For example, the third convergent of ![pi=[3;7,15]](https://mathworld.wolfram.com/images/equations/Convergent/Inline7.gif) is
is
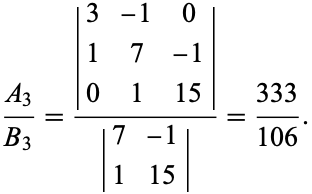 |
(4) |
In the Wolfram Language, Convergents[terms] gives a list of the convergents corresponding to the specified list of continued fraction terms, while Convergents[x, n] gives the first 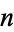 convergents for a number
convergents for a number 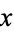 .
.
Consider the convergents 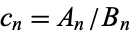 of a simple continued fraction
of a simple continued fraction ![[b_0;b_1,b_2,...]](https://mathworld.wolfram.com/images/equations/Convergent/Inline11.gif) , and define
, and define
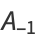 |
 |
 |
(5) |
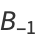 |
 |
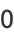 |
(6) |
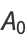 |
 |
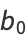 |
(7) |
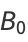 |
 |
 |
(8) |
Then subsequent terms can be calculated from the recurrence relations
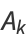 |
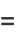 |
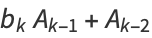 |
(9) |
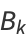 |
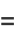 |
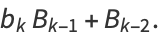 |
(10) |
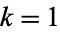 , 2, ...,
, 2, ..., 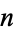 .
.
For a generalized continued fraction 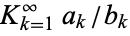 , the recurrence generalizes to
, the recurrence generalizes to
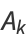 |
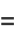 |
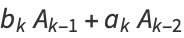 |
(11) |
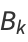 |
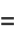 |
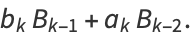 |
(12) |
The continued fraction fundamental recurrence relation for a simple continued fraction is
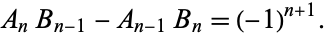 |
(13) |
It is also true that if 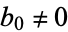 ,
,
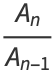 |
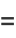 |
![[b_n;b_(n-1),...,b_0]](https://mathworld.wolfram.com/images/equations/Convergent/Inline42.gif) |
(14) |
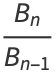 |
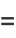 |
![[b_n;b_(n-1),...,b_1].](https://mathworld.wolfram.com/images/equations/Convergent/Inline45.gif) |
(15) |
Furthermore,
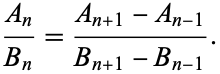 |
(16) |
Also, if a convergent 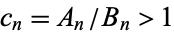 , then
, then
![(B_n)/(A_n)=[0;b_0,b_1,...,b_n].](https://mathworld.wolfram.com/images/equations/Convergent/NumberedEquation7.gif) |
(17) |
Similarly, if 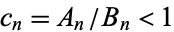 , then
, then 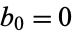 and
and
![(B_n)/(A_n)=[0;b_1,...,b_n].](https://mathworld.wolfram.com/images/equations/Convergent/NumberedEquation8.gif) |
(18) |
The convergents 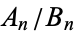 also satisfy
also satisfy
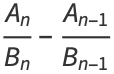 |
 |
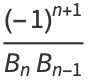 |
(19) |
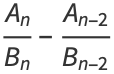 |
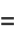 |
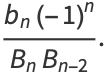 |
(20) |
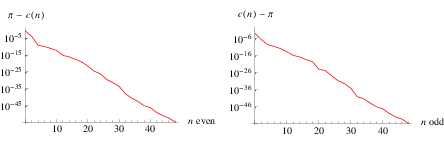
Plotted above on semilog scales are 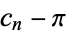 (
(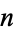 even; left figure) and
even; left figure) and 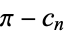 (
(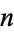 odd; right figure) as a function of
odd; right figure) as a function of 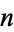 for the convergents of
for the convergents of 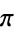 . In general, the even convergents
. In general, the even convergents 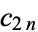 of an infinite simple continued fraction for a number
of an infinite simple continued fraction for a number 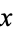 form an increasing sequence, and the odd convergents
form an increasing sequence, and the odd convergents 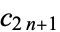 form a decreasing sequence (so any even convergent is less than any odd convergent). Summarizing,
form a decreasing sequence (so any even convergent is less than any odd convergent). Summarizing,
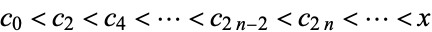 |
(21) |
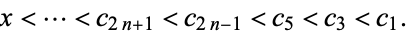 |
(22) |
Furthermore, each convergent for 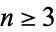 lies between the two preceding ones. Each convergent is nearer to the value of the infinite continued fraction than the previous one. In addition, for a number
lies between the two preceding ones. Each convergent is nearer to the value of the infinite continued fraction than the previous one. In addition, for a number ![x=[b_0;b_1,b_2,...]](https://mathworld.wolfram.com/images/equations/Convergent/Inline66.gif) ,
,
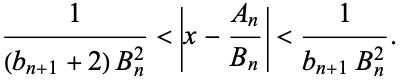 |
(23) |
REFERENCES:
D'Angelo, J. P. and West, D. B. Mathematical Thinking: Problem-Solving and Proofs, 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 2000.
Liberman, H. Simple Continued Fractions: An Elementary to Research Level Approach. SMD Stock Analysts, pp. II-9-II-10, 2003.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|