


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-11-2019
Date: 20-5-2020
Date: 20-1-2021
|
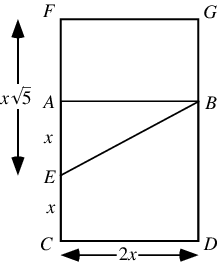
Given a rectangle having sides in the ratio 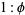 , the golden ratio
, the golden ratio 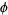 is defined such that partitioning the original rectangle into a square and new rectangle results in a new rectangle having sides with a ratio
is defined such that partitioning the original rectangle into a square and new rectangle results in a new rectangle having sides with a ratio 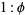 . Such a rectangle is called a golden rectangle. Euclid used the following construction to construct them. Draw the square
. Such a rectangle is called a golden rectangle. Euclid used the following construction to construct them. Draw the square 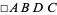 , call
, call 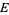 the midpoint of
the midpoint of 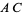 , so that
, so that 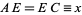 . Now draw the segment
. Now draw the segment 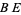 , which has length
, which has length
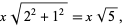 |
(1) |
and construct 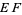 with this length. Now complete the rectangle
with this length. Now complete the rectangle 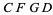 , which is golden since
, which is golden since
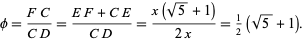 |
(2) |
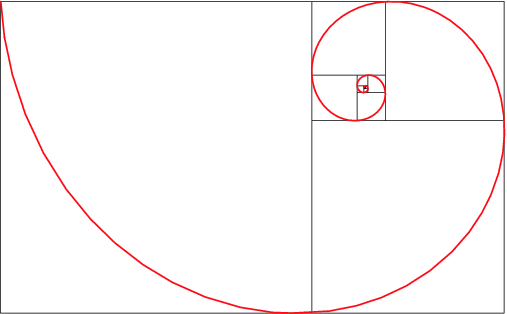
Successive points dividing a golden rectangle into squares lie on a logarithmic spiral (Wells 1991, p. 39; Livio 2002, p. 119) which is sometimes known as the golden spiral.

The spiral is not actually tangent at these points, however, but passes through them and intersects the adjacent side, as illustrated above.
If the top left corner of the original square is positioned at (0, 0), the center of the spiral occurs at the position
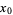 |
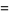 |
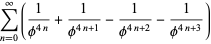 |
(3) |
 |
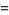 |
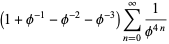 |
(4) |
 |
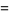 |
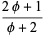 |
(5) |
 |
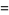 |
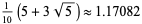 |
(6) |
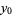 |
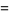 |
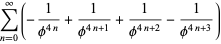 |
(7) |
 |
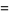 |
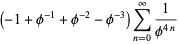 |
(8) |
 |
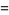 |
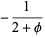 |
(9) |
 |
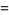 |
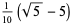 |
(10) |
 |
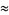 |
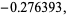 |
(11) |
and the parameters of the spiral 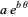 are given by
are given by
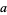 |
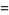 |
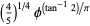 |
(12) |
 |
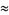 |
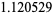 |
(13) |
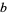 |
 |
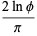 |
(14) |
 |
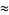 |
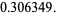 |
(15) |
REFERENCES:
Bicknell, M.; and Hoggatt, V. E. Jr. "Golden Triangles, Rectangles, and Cuboids." Fib. Quart. 7, 73-91, 1969.
Cook, T. A. The Curves of Life, Being an Account of Spiral Formations and Their Application to Growth in Nature, To Science and to Art. New York: Dover, 1979.
Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 70, 1989.
Kabai, S. Mathematical Graphics I: Lessons in Computer Graphics Using Mathematica. Püspökladány, Hungary: Uniconstant, p. 79, 2002.
Livio, M. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. New York: Broadway Books, p. 85, 2002.
Pappas, T. "The Golden Rectangle." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 102-106, 1989.
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 45-47, 1999.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 88, 1991.
Williams, R. The Geometrical Foundation of Natural Structure: A Source Book of Design. New York: Dover, p. 53, 1979.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|