
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-7-2019
Date: 14-10-2019
Date: 9-8-2019
|
Let 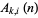 denote the number of partitions into
denote the number of partitions into 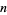 parts not congruent to 0,
parts not congruent to 0, 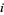 , or
, or 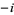 (mod
(mod 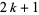 ). Let
). Let 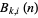 denote the number of partitions of
denote the number of partitions of 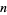 wherein
wherein
1. 1 appears as a part at most 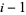 times.
times.
2. The total number of appearances of 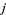 and
and 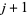 (i.e., any two consecutive integers) together is at most
(i.e., any two consecutive integers) together is at most 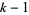 .
.
Then Gordon's partition theorem states that for 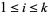 ,
,
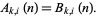 |
The first Rogers-Ramanujan identity corresponds to 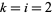 , and the second to
, and the second to 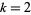 ,
, 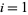 .
.
REFERENCES:
Andrews, G. E. and Santos, J. P. O. "Rogers-Ramanujan Type Identities for Partitions with Attached Odd Parts." Ramanujan J. 1, 91-99, 1997.
Gordon, B. "A Combinatorial Generalization of the Rogers-Ramanujan Identities." Amer. J. Math. 83, 393-399, 1961.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|