


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-9-2019
Date: 17-9-2018
Date: 25-4-2019
|
The Zernike polynomials are a set of orthogonal polynomials that arise in the expansion of a wavefront function for optical systems with circular pupils. The odd and even Zernike polynomials are given by
 |
(1) |
where the radial function 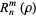 is defined for
is defined for 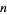 and
and 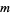 integers with
integers with 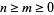 by
by
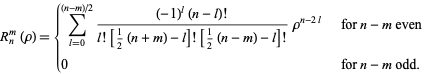 |
(2) |
Here, 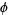 is the azimuthal angle with
is the azimuthal angle with 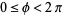 and
and 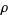 is the radial distance with
is the radial distance with 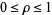 (Prata and Rusch 1989). The even and odd polynomials are sometimes also denoted
(Prata and Rusch 1989). The even and odd polynomials are sometimes also denoted
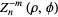 |
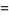 |
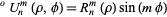 |
(3) |
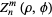 |
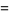 |
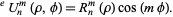 |
(4) |
Zernike polynomials are implemented in the Wolfram Language as ZernikeR[n, m, rho].
Other closed forms for 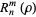 include
include
 |
(5) |
for 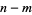 odd and
odd and 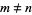 , where
, where 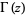 is the gamma function and
is the gamma function and 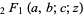 is a hypergeometric function. This can also be written in terms of the Jacobi polynomial
is a hypergeometric function. This can also be written in terms of the Jacobi polynomial 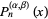 as
as
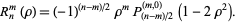 |
(6) |
The first few nonzero radial polynomials are
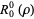 |
 |
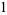 |
(7) |
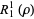 |
 |
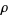 |
(8) |
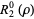 |
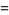 |
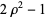 |
(9) |
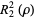 |
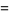 |
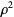 |
(10) |
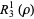 |
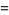 |
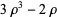 |
(11) |
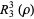 |
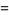 |
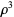 |
(12) |
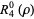 |
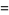 |
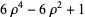 |
(13) |
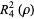 |
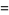 |
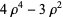 |
(14) |
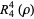 |
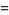 |
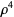 |
(15) |
(Born and Wolf 1989, p. 465).
The radial functions satisfy the orthogonality relation
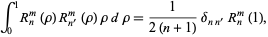 |
(16) |
where 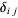 is the Kronecker delta, and are related to the Bessel function of the first kind by
is the Kronecker delta, and are related to the Bessel function of the first kind by
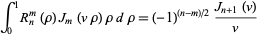 |
(17) |
(Born and Wolf 1989, p. 466). The radial Zernike polynomials have the generating function
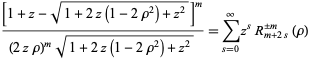 |
(18) |
(correcting the typo of Born and Wolf) and are normalized so that
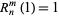 |
(19) |
(Born and Wolf 1989, p. 465).
The Zernike polynomials also satisfy the recurrence relations
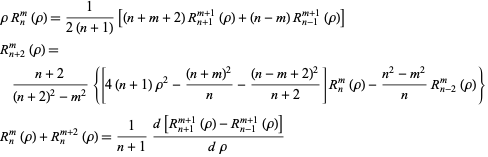 |
(20) |
(Prata and Rusch 1989). The coefficients 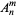 and
and 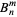 in the expansion of an arbitrary radial function
in the expansion of an arbitrary radial function 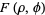 in terms of Zernike polynomials
in terms of Zernike polynomials
![F(rho,phi)=sum_(m=0)^inftysum_(n=m)^infty[A_n^m^oU_n^m(rho,phi)+B_n^m^eU_n^m(rho,phi)]](http://mathworld.wolfram.com/images/equations/ZernikePolynomial/NumberedEquation10.gif) |
(21) |
are given by
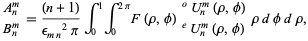 |
(22) |
where
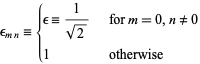 |
(23) |
Let a "primary" aberration be given by
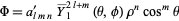 |
(24) |
with 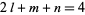 and where
and where 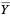 is the complex conjugate of
is the complex conjugate of 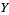 , and define
, and define
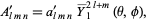 |
(25) |
giving
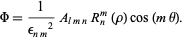 |
(26) |
Then the types of primary aberrations are given in the following table (Born and Wolf 1989, p. 470).
| aberration | 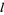 |
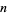 |
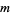 |
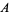 |
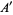 |
| spherical aberration | 0 | 4 | 0 | 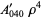 |
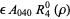 |
| coma | 0 | 3 | 1 | 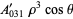 |
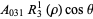 |
| astigmatism | 0 | 2 | 2 | 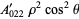 |
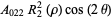 |
| field curvature | 1 | 2 | 0 | 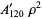 |
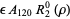 |
| distortion | 1 | 1 | 1 | 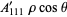 |
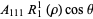 |
REFERENCES:
Bezdidko, S. N. "The Use of Zernike Polynomials in Optics." Sov. J. Opt. Techn. 41, 425, 1974.
Bhatia, A. B. and Wolf, E. "On the Circle Polynomials of Zernike and Related Orthogonal Sets." Proc. Cambridge Phil. Soc. 50, 40, 1954.
Born, M. and Wolf, E. "The Diffraction Theory of Aberrations." Ch. 9 in Principles of Optics: Electromagnetic Theory of Propagation, Interference, and Diffraction of Light, 6th ed. New York: Pergamon Press, pp. 459-490, 1989.
Mahajan, V. N. "Zernike Circle Polynomials and Optical Aberrations of Systems with Circular Pupils." In Engineering and Lab. Notes 17 (Ed. R. R. Shannon), p. S-21, Aug. 1994.
Prata, A. and Rusch, W. V. T. "Algorithm for Computation of Zernike Polynomials Expansion Coefficients." Appl. Opt. 28, 749-754, 1989.
Wang, J. Y. and Silva, D. E. "Wave-Front Interpretation with Zernike Polynomials." Appl. Opt. 19, 1510-1518, 1980.
Wyant, J. C. "Zernike Polynomials." http://wyant.optics.arizona.edu/zernikes/zernikes.htm.
Zernike, F. "Beugungstheorie des Schneidenverfahrens und seiner verbesserten Form, der Phasenkontrastmethode." Physica 1, 689-704, 1934.
Zhang, S. and Shannon, R. R. "Catalog of Spot Diagrams." Ch. 4 in Applied Optics and Optical Engineering, Vol. 11. New York: Academic Press, p. 201, 1992.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|