المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Chi |
 2018
 04:29 مساءً
date: 29-7-2019 |
Author : Abramowitz, M. and Stegun, I. A. 
Book or Source : "Sine and Cosine Integrals." §5.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover 
Page and Part : pp. 231-233|
Read More
Date: 22-5-2019
1714
Date: 25-7-2019
1632
Date: 29-9-2018
3080
|
 |
 |
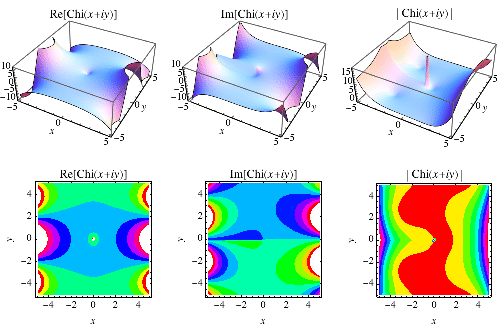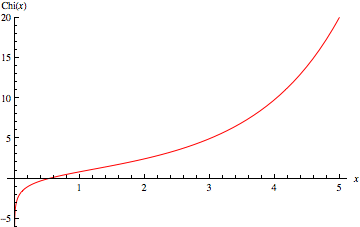
The hyperbolic cosine integral, often called the "Chi function" for short, is defined by
 |
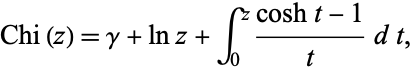(1) |
where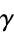 
is the Euler-Mascheroni constant. The function is given by the Wolfram Language command CoshIntegral[z].
The Chi function has a unique real root at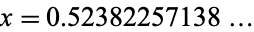 
(OEIS A133746).
The derivative of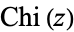 
is
 |
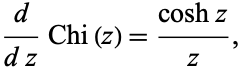(2) |
and the integral is
 |
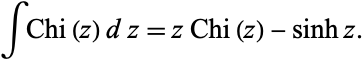(3) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Sine and Cosine Integrals." §5.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 231-233, 1972.
Sloane, N. J. A. Sequence A133746 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|
