


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-4-2018
Date: 28-7-2019
Date: 9-6-2019
|
Lauricella functions are generalizations of the Gauss hypergeometric functions to multiple variables. Four such generalizations were investigated by Lauricella (1893), and more fully by Appell and Kampé de Fériet (1926, p. 117). Let 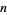 be the number of variables, then the Lauricella functions are defined by
be the number of variables, then the Lauricella functions are defined by
 |
If 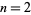 , then these functions reduce to the Appell hypergeometric functions
, then these functions reduce to the Appell hypergeometric functions 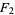 ,
, 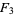 ,
, 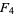 , and
, and 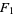 , respectively. If
, respectively. If 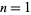 , all four become the Gauss hypergeometric function
, all four become the Gauss hypergeometric function 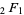 (Exton 1978, p. 29).
(Exton 1978, p. 29).
REFERENCES:
Appell, P. and Kampé de Fériet, J. Fonctions hypergéométriques et hypersphériques: polynomes d'Hermite. Paris: Gauthier-Villars, 1926.
Erdélyi, A. "Hypergeometric Functions of Two Variables." Acta Math. 83, 131-164, 1950.
Exton, H. Ch. 5 in Multiple Hypergeometric Functions and Applications. New York: Wiley, 1976.
Exton, H. "The Lauricella Functions and Their Confluent Forms," "Convergence," and "Systems of Partial Differential Equations." §1.4.1-1.4.3 in Handbook of Hypergeometric Integrals: Theory, Applications, Tables, Computer Programs. Chichester, England: Ellis Horwood, pp. 29-31, 1978.
Lauricella, G. "Sulla funzioni ipergeometriche a più variabili." Rend. Circ. Math. Palermo 7, 111-158, 1893.
Srivastava, H. M. and Karlsson, P. W. Multiple Gaussian Hypergeometric Series. Chichester, England: Ellis Horwood, 1985.



|
|
|
|
تحذير من "عادة" خلال تنظيف اللسان.. خطيرة على القلب
|
|
|
|
|
|
|
دراسة علمية تحذر من علاقات حب "اصطناعية" ؟!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تحذّر من خطورة الحرب الثقافية والأخلاقية التي تستهدف المجتمع الإسلاميّ
|
|
|