المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Gamma Product |
 1384
 11:58 صباحاً
date: 22-5-2019 |
Author : Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I 
Book or Source : Integrals and Series, Vol. 1: Elementary Functions. New York: Gordon and Breach, 1986. 
Page and Part : ...|
Read More
Date: 12-10-2018
1597
Date: 3-6-2019
1249
Date: 24-3-2019
1513
|
The gamma product (e.g., Prudnikov et al. 1986, pp. 22 and 792), is defined by
![Gamma[a_1,...,a_m; b_1,...,b_n]=(Gamma(a_1)...Gamma(a_m))/(Gamma(b_1)...Gamma(b_n)),](http://mathworld.wolfram.com/images/equations/GammaProduct/NumberedEquation1.gif) |
where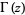 
is a gamma function.
REFERENCES:
Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. Integrals and Series, Vol. 1: Elementary Functions. New York: Gordon and Breach, 1986.
|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
شعبة فاطمة بنت أسد (عليها السلام) تنظم دورة تخصصية في أحكام التلاوة
|
|
|
