Superfactorial

The superfactorial of 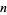 is defined by Pickover (1995) as

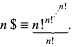(1)

The first two values are 1 and 4, but subsequently grow so rapidly that 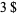 already has a huge number of digits.

Sloane and Plouffe (1995) define the superfactorial by

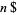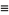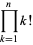			(2)
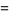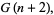			(3)

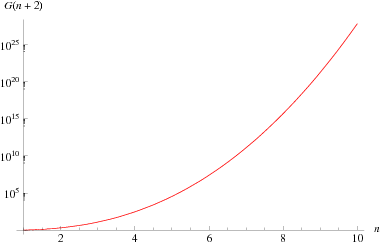
which is equivalent to the integral values of the Barnes G-function. The values for 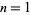, 2, ... are 1, 1, 2, 12, 288, 34560, ... (OEIS A000178). This function has an unexpected connection with Bell numbers.

REFERENCES:

Fletcher, A.; Miller, J. C. P.; Rosenhead, L.; and Comrie, L. J. An Index of Mathematical Tables, Vol. 1. Oxford, England: Blackwell, p. 50, 1962.

Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, p. 231 1994.

Pickover, C. A. Keys to Infinity. New York: Wiley, p. 102, 1995.

Radoux, C. "Query 145." Not. Amer. Math. Soc. 25, 197, 1978.

Ryser, H. J. Combinatorial Mathematics. Buffalo, NY: Math. Assoc. Amer., p. 53, 1963.

Sloane, N. J. A. Sequence A000178/M2049 in "The On-Line Encyclopedia of Integer Sequences."