


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-6-2019
Date: 25-4-2019
Date: 23-6-2019
|
When the elliptic modulus 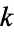 has a singular value, the complete elliptic integrals may be computed in analytic form in terms of gamma functions. Abel (quoted in Whittaker and Watson 1990, p. 525) proved that whenever
has a singular value, the complete elliptic integrals may be computed in analytic form in terms of gamma functions. Abel (quoted in Whittaker and Watson 1990, p. 525) proved that whenever
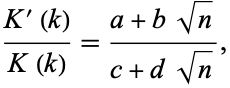 |
(1) |
where 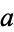 ,
, 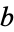 ,
, 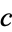 ,
, 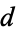 , and
, and 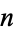 are integers,
are integers, 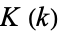 is a complete elliptic integral of the first kind, and
is a complete elliptic integral of the first kind, and 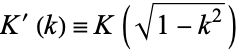 is the complementary complete elliptic integral of the first kind, then the elliptic modulus
is the complementary complete elliptic integral of the first kind, then the elliptic modulus 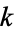 is the root of an algebraic equation with integer coefficients.
is the root of an algebraic equation with integer coefficients.
A elliptic modulus 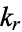 such that
such that
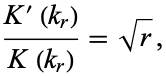 |
(2) |
is called a singular value of the elliptic integral. The elliptic lambda function 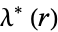 gives the value of
gives the value of 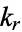 .
.
Selberg and Chowla (1967) showed that 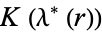 and
and 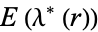 are expressible in terms of a finite number of gamma functions. The complete elliptic integrals of the second kind
are expressible in terms of a finite number of gamma functions. The complete elliptic integrals of the second kind 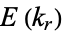 and
and 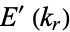 can be expressed in terms of
can be expressed in terms of 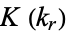 and
and 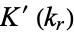 with the aid of the elliptic alpha function
with the aid of the elliptic alpha function 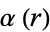 .
.
Values of 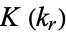 for small integer
for small integer 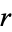 in terms of gamma functions
in terms of gamma functions 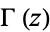 are summarized below.
are summarized below.
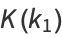 |
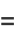 |
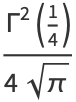 |
(3) |
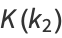 |
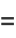 |
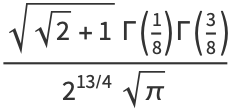 |
(4) |
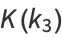 |
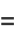 |
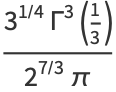 |
(5) |
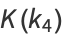 |
 |
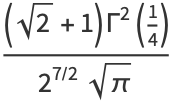 |
(6) |
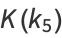 |
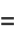 |
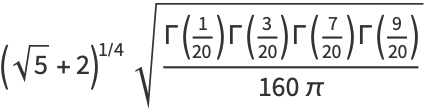 |
(7) |
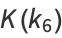 |
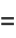 |
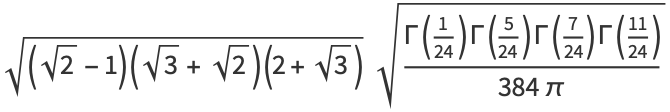 |
(8) |
 |
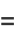 |
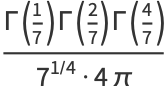 |
(9) |
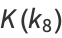 |
 |
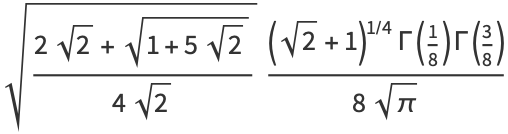 |
(10) |
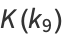 |
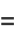 |
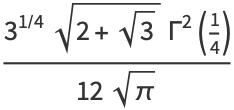 |
(11) |
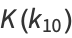 |
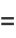 |
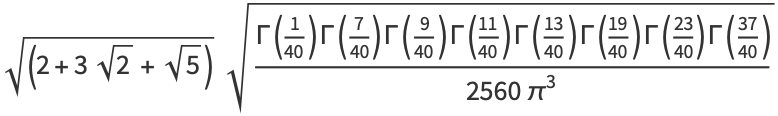 |
(12) |
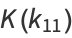 |
 |
![[2+(17+3sqrt(33))^(1/3)-(3sqrt(33)-17)^(1/3)]^2(Gamma(1/(11))Gamma(3/(11))Gamma(4/(11))Gamma(5/(11))Gamma(9/(11)))/(11^(1/4)144pi^2)](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValue/Inline55.gif) |
(13) |
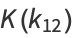 |
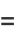 |
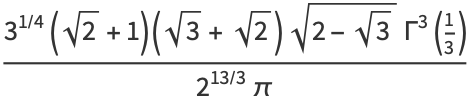 |
(14) |
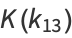 |
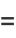 |
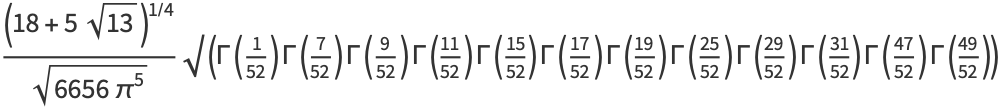 |
(15) |
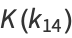 |
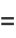 |
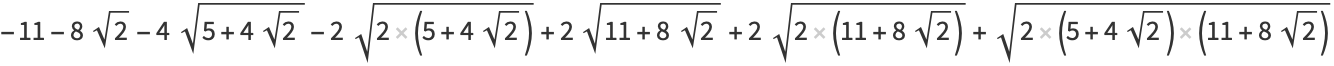 |
(16) |
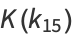 |
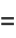 |
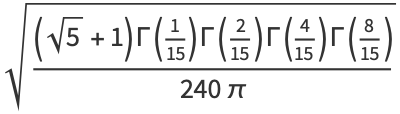 |
(17) |
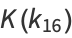 |
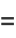 |
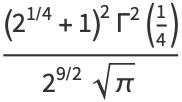 |
(18) |
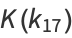 |
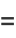 |
![C_1[(Gamma(1/(68))Gamma(3/(68))Gamma(7/(68))Gamma((11)/(68))Gamma((13)/(68)))/(Gamma(5/(68))Gamma((15)/(68))Gamma((19)/(68))Gamma((29)/(68)))]^(1/4)[Gamma((21)/(68))Gamma((25)/(68))Gamma((27)/(68))Gamma((31)/(68))Gamma((33)/(68))]^(1/4)](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValue/Inline73.gif) |
(19) |
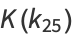 |
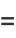 |
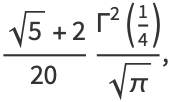 |
(20) |
where 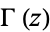 is the gamma function and
is the gamma function and 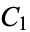 is an algebraic number (Borwein and Borwein 1987, p. 298).
is an algebraic number (Borwein and Borwein 1987, p. 298).
Borwein and Zucker (1992) give amazing expressions for singular values of complete elliptic integrals in terms of central beta functions
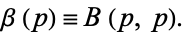 |
(21) |
Furthermore, they show that 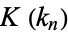 is always expressible in terms of these functions for
is always expressible in terms of these functions for 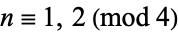 . In such cases, the
. In such cases, the 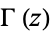 functions appearing in the expression are of the form
functions appearing in the expression are of the form 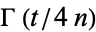 where
where 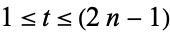 and
and 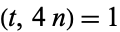 . The terms in the numerator depend on the sign of the Kronecker symbol
. The terms in the numerator depend on the sign of the Kronecker symbol 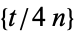 . Values for the first few
. Values for the first few 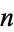 are
are
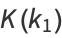 |
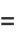 |
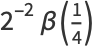 |
(22) |
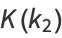 |
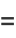 |
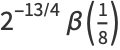 |
(23) |
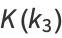 |
 |
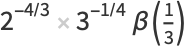 |
(24) |
 |
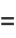 |
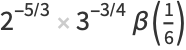 |
(25) |
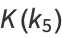 |
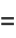 |
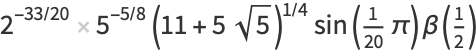 |
(26) |
 |
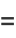 |
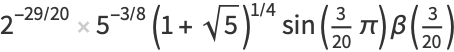 |
(27) |
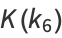 |
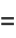 |
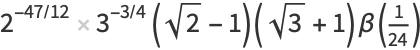 |
(28) |
 |
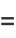 |
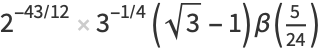 |
(29) |
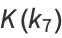 |
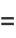 |
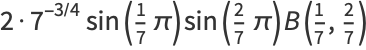 |
(30) |
 |
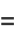 |
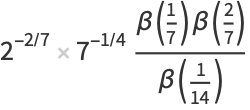 |
(31) |
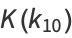 |
 |
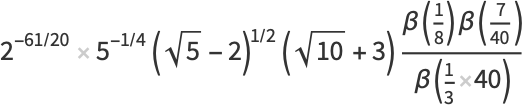 |
(32) |
 |
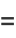 |
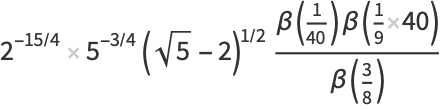 |
(33) |
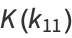 |
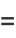 |
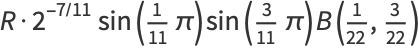 |
(34) |
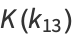 |
 |
![2^(-3)13^(-5/8)(5sqrt(13)+18)^(1/4)[tan(1/(52)pi)tan(3/(52)pi)tan(9/(52)pi)]^(1/2)(beta(1/(52))beta(9/(52)))/(beta((23)/(52)))](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValue/Inline128.gif) |
(35) |
 |
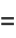 |
![sqrt(sqrt(4sqrt(2)+2)+sqrt(2)+sqrt(2sqrt(2)-1))·2^(-13/4)7^(-3/8)×[(tan(5/(56)pi)tan((13)/(56)pi))/(tan((11)/(56)pi))]^(1/4)sqrt((beta(5/(56))beta((13)/(56))beta(1/8))/(beta((11)/(56))))](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValue/Inline131.gif) |
(36) |
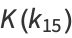 |
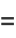 |
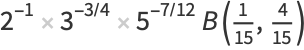 |
(37) |
 |
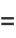 |
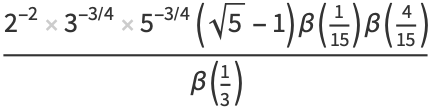 |
(38) |
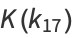 |
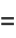 |
![C_2[(beta(1/(68))beta(3/(68))beta(7/(68))beta(9/(68))beta((11)/(68))beta((13)/(68)))/(beta(5/(68))beta((15)/(68)))]^(1/4),](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValue/Inline140.gif) |
(39) |
where 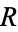 is the real root of
is the real root of
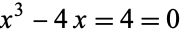 |
(40) |
and 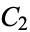 is an algebraic number (Borwein and Zucker 1992). Note that
is an algebraic number (Borwein and Zucker 1992). Note that 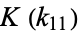 is the only value in the above list which cannot be expressed in terms of central beta functions.
is the only value in the above list which cannot be expressed in terms of central beta functions.
Using the elliptic alpha function, the elliptic integrals of the second kind can also be found from
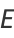 |
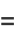 |
![pi/(4sqrt(r)K)+[1-(alpha(r))/(sqrt(r))]K](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValue/Inline146.gif) |
(41) |
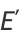 |
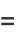 |
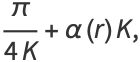 |
(42) |
and by definition,
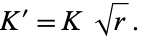 |
(43) |
REFERENCES:
Abel, N. H. "Recherches sur les fonctions elliptiques." J. reine angew. Math. 3, 160-190, 1828. Reprinted in Abel, N. H. Oeuvres Completes (Ed. L. Sylow and S. Lie). New York: Johnson Reprint Corp., p. 377, 1988.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 139 and 298, 1987.
Borwein, J. M. and Zucker, I. J. "Elliptic Integral Evaluation of the Gamma Function at Rational Values of Small Denominator." IMA J. Numerical Analysis 12, 519-526, 1992.
Bowman, F. Introduction to Elliptic Functions, with Applications. New York: Dover, pp. 75, 95, and 98, 1961.
Glasser, M. L. and Wood, V. E. "A Closed Form Evaluation of the Elliptic Integral." Math. Comput. 22, 535-536, 1971.
Selberg, A. and Chowla, S. "On Epstein's Zeta-Function." J. reine angew. Math. 227, 86-110, 1967.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 524-528, 1990.
Wrigge, S. "An Elliptic Integral Identity." Math. Comput. 27, 837-840, 1973.
Zucker, I. J. "The Evaluation in Terms of  -Functions of the Periods of Elliptic Curves Admitting Complex Multiplication." Math. Proc. Cambridge Philos. Soc. 82, 111-118, 1977.
-Functions of the Periods of Elliptic Curves Admitting Complex Multiplication." Math. Proc. Cambridge Philos. Soc. 82, 111-118, 1977.
Zucker, I. J. and Joyce, G. S. "Special Values of the Hypergeometric Series II." Math. Proc. Cambridge Philos. Soc. 131, 309-319, 2001.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|