
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-2-2019
Date: 17-2-2019
Date: 6-3-2017
|
If the coefficients of the polynomial
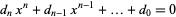 |
(1) |
are specified to be integers, then rational roots must have a numerator which is a factor of 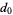 and a denominatorwhich is a factor of
and a denominatorwhich is a factor of 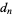 (with either sign possible). This follows since a polynomial of polynomial order
(with either sign possible). This follows since a polynomial of polynomial order 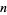 with
with 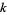 rational roots can be expressed as
rational roots can be expressed as
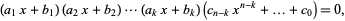 |
(2) |
where the roots are 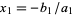 ,
, 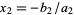 , ..., and
, ..., and 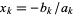 . Factoring out the
. Factoring out the 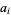 s,
s,
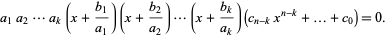 |
(3) |
Now, multiplying through,
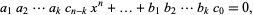 |
(4) |
where we have not bothered with the other terms. Since the first and last coefficients are 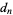 and
and 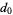 , all the rational roots of equation (1) are of the form [factors of
, all the rational roots of equation (1) are of the form [factors of 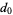 ]/[factors of
]/[factors of 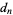 ].
].
REFERENCES:
Bold, B. Famous Problems of Geometry and How to Solve Them. New York: Dover, p. 34, 1982.
Niven, I. M. Numbers: Rational and Irrational. New York: Random House, 1961.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|