Generalized Hypergeometric Differential Equation

The generalized hypergeometric function

satisfies the equation

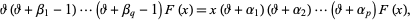where 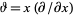 is the differential operator.

REFERENCES:

Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, p. 26, 1998.

Miller, W. Jr. Symmetry and Separation of Variables. Reading, MA: Addison-Wesley, p. 271, 1977.

Rainville, E. D. Special Functions. New York: Chelsea, 1971.

Slater, L. J. Confluent Hypergeometric Functions. Cambridge, England: Cambridge University Press, p. 1, 1960.

Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 128, 1997.