


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-12-2018
Date: 22-5-2018
Date: 5-7-2018
|
The problem of finding the connection between a continuous function 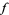 on the boundary
on the boundary 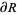 of a region
of a region 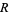 with a harmonic function taking on the value
with a harmonic function taking on the value 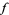 on
on 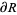 . In general, the problem asks if such a solution exists and, if so, if it is unique. The Dirichlet problem is extremely important in mathematical physics (Courant and Hilbert 1989, pp. 179-180 and 240; Logan 1997; Krantz 1999b).
. In general, the problem asks if such a solution exists and, if so, if it is unique. The Dirichlet problem is extremely important in mathematical physics (Courant and Hilbert 1989, pp. 179-180 and 240; Logan 1997; Krantz 1999b).
If 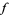 is a continuous function on the boundary of the open unit disk
is a continuous function on the boundary of the open unit disk 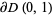 , then define
, then define
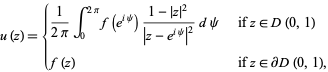 |
(1) |
where 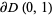 is the boundary of
is the boundary of 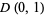 . Then
. Then 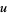 is continuous on the closed unit disk
is continuous on the closed unit disk 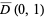 and harmonic on
and harmonic on 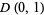 (Krantz 1999a, p. 93).
(Krantz 1999a, p. 93).
For the case of rational boundary data without poles, the resulting solution of the Dirichlet problem is also rational (Ebenfelt and Viscardi 2005), the proof of which led to Viscardi winning the 2005-2006 Siemens-Westinghouse competition (Siemens Foundation 2005; Mathematical Association of America 2006).
REFERENCES:
Courant, R. and Hilbert, D. Methods of Mathematical Physics, Vol. 1. New York: Wiley, pp. 179-180 and 240, 1989.
Ebenfelt, P. and Viscardi, M. "On the Solution of the Dirichlet Problem with Rational Holomorphic Boundary Data." Comput. Meth. Func. Th. 5, 445-457, 2005. http://www.heldermann.de/CMF/CMF05/CMF052/cmf05027.htm.
Krantz, S. G. "The Dirichlet Problem" and "Application of Conformal Mapping to the Dirichlet Problem." §7.3.3, 7.7.1, and 14.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 93, 97-98, and 164-168, 1999a.
Krantz, S. G. A Panorama of Harmonic Analysis. Washington, DC: Math. Assoc. Amer., 1999b.
Logan, J. D. Applied Mathematics, 2nd ed. New York: Wiley, 1997.
Mathematical Association of America. "Mathematics Student Wins the Siemens-Westinghouse Competition." Jan. 9, 2006. http://www.maa.org/news/010906westinghouse.html.
Siemens Foundation. "2005 Siemens Competition Nationals." http://www.siemens-foundation.org/competition/2005/2005Nationals.htm#Michael.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|