Stretched Harmonic Oscillator
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 2 , p 71
22-8-2016
1551
Stretched Harmonic Oscillator
Use WKB in one dimension to calculate the eigenvalues of a particle of mass m in the following potential (see Figure 1.1):
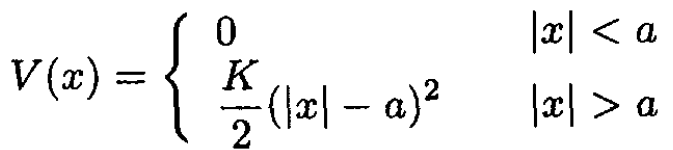(i)
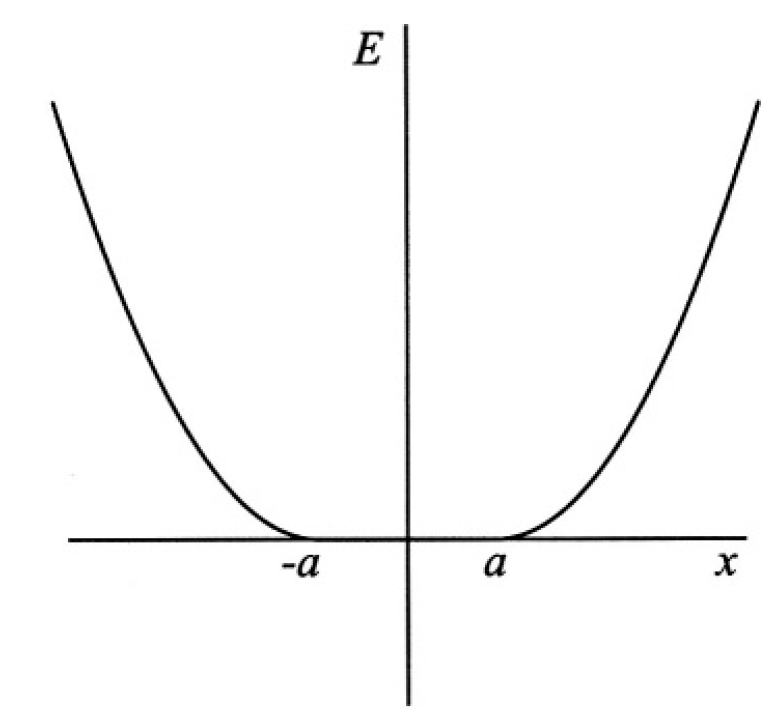
Figure 1.1
SOLUTION
The turning point C is where the argument of k(x) = 0. For the present potential the turning point is
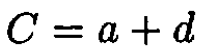(1)
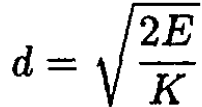(2)
In the interval –a < x < a then V(x) = 0, k(x) is a constant, and the integral is just 2ak. The potential V(x) is nonzero in the two intervals –C < x < -a and a < x < C. Since the WKB integral is symmetric, we get
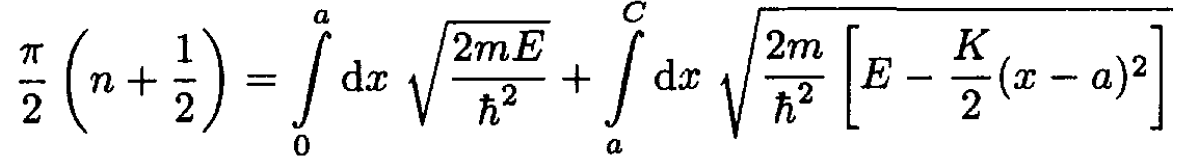(3)
To evaluate the second integral, change variables to y = x – a:
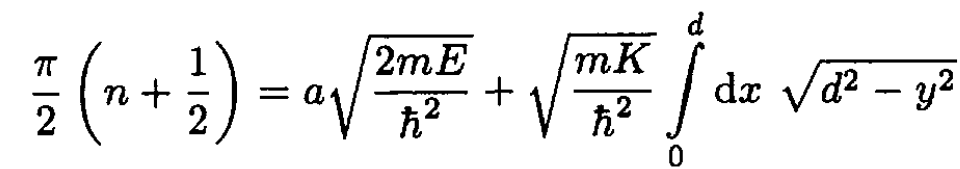(4)
The last integral equals d2π/4. Writing K = mω2, we find
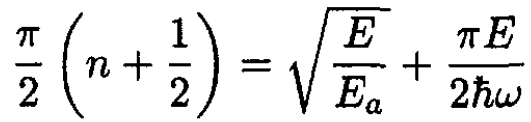(5)
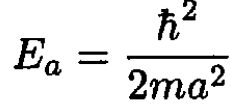(6)
We have to determine E. Equation (5) is a quadratic equation for the variable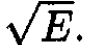 
Solving the quadratic by the usual formula gives the final result:
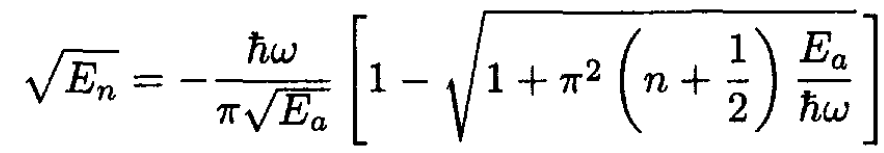(7)
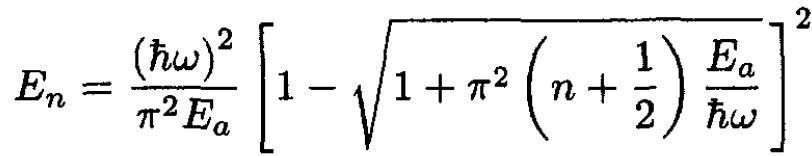(8)
الاكثر قراءة في مواضيع اخرى
اخر الاخبار
اخبار العتبة العباسية المقدسة
