Superconducting Sphere in Magnetic Field

A superconducting (Type I) spherical shell of radius R is placed in a uniform magnetic field B₀ (B₀ << H_c, H_c, the critical field). Find

a) the magnetic field everywhere outside the shell

b) the surface current density

Hint: Inside, B = 0.

SOLUTION

a) Prom symmetry considerations, it is clear that the current would flow on the surface of the shell perpendicular to the applied magnetic field. As for any ellipsoid in a uniform electric or magnetic field, we can assume that the field outside the shell produced by these currents is equivalent to a magnetic dipole moment m placed in the center of the shell. For

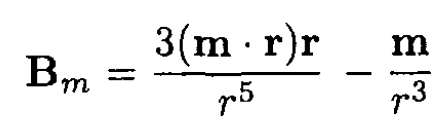
The total field outside is then B = B_m + B₀. The boundary condition on the surface at an arbitrary point gives

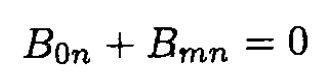
The normal component of B is continuous and inside B = 0. From the boundary conditions on the surface at an arbitrary angle θ between the direction of B₀ and the normal n (see Figure 1.1) we have

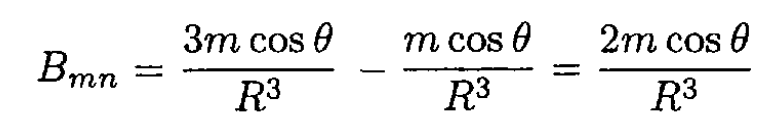(1)

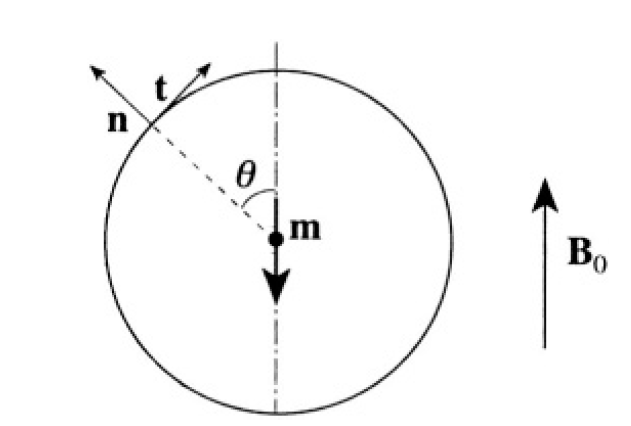
Figure 1.1

Hence

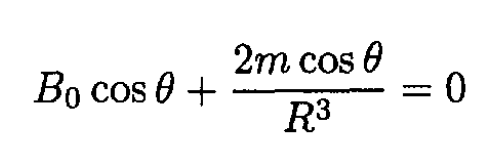(2)

At m = -(R³/2) B₀, where R is the radius of the spherical shell, the boundary conditions are satisfied on the surface of the shell. Therefore,

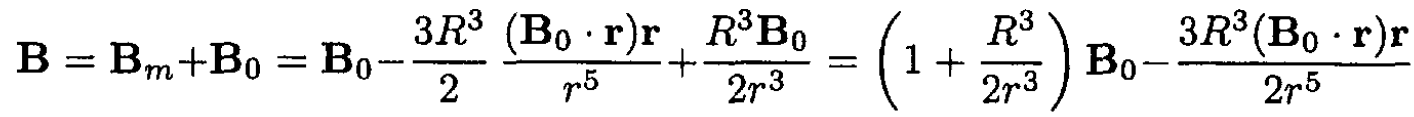
b) The surface current density J_s can be found by using tangential H component continuity:

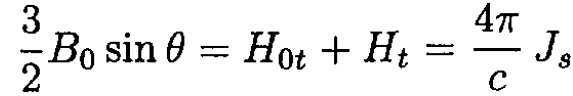
and therefore J_s(θ) = 3cB₀ sin θ/8π. This solution is only true while B < 2/3 H_c, and the whole sphere is superconducting. When B > 2/3 H_c the field at the equator exceeds H_c, and the sphere goes into an intermediate state.

اخر الاخبار

اخبار العتبة العباسية المقدسة

تزامنًا مع حلول شهر ربيع الأول.. العتبة العباسية المقدسة ترفع مظاهر الحزن والسواد في المرقد الطاهر

بعد انتهاء شهري المحرم وصفر.. قسم الصيانة يباشر إدامة الثريات واستبدال مصابيح المرقد الطاهر

قسم الشؤون الخدمية يشرع بإدامة آليّات النظافة عقب انتهاء زيارة الأربعين

موكب عزاء الشعراء والرواديد ينظم مسيرة عزائية في ختام شهري الأحزان المحرم الحرام وصفر

المزيد

الآخبار الصحية

العنب.. فاكهة صغيرة بمفعول "خارق" للقلب والدماغ

دراسة تحدد "الحلقة المفقودة".. تسبب ارتفاع ضغط الدم

هذه الأطعمة تحمي دماغك من الشيخوخة وتزيد حدة الذكاء

خبراء يحذرون من مخاطر "الدهون المخفية" على القلب

المزيد

الآخبار التكنلوجية

الأرصاد الجوية تلجأ إلى الذكاء الاصطناعي.. لأي غرض؟

في منزلك.. "تعديل بسيط" يخفض ضغط الدم بشكل طبيعي

"ميزة جديدة" من إنستغرام تنافس تيك توك.. طال انتظارها

غوغل في مأزق.. بيانات 2.5 مليار مستخدم بقبضة القراصنة

المزيد

مواضيع ذات صلة

جسيمات التماثل الفائق الفوتينوات ، سكواركات ..المادة الظل.. الأكسيونات ..إلخ .

ريادةالانسان للفضاء -قدرة الله في خلق الطيور(كيف الهمت الطيور الانسان )

التجريبية المنطقية وميكانيكا الكم: رؤية كاسيرر بين العلم والفلسفة

المفاهيم الفيزيائية بين الدقة العلمية والتأويل الفلسفي

"توحيد العلوم عبر استبعاد الميتافيزيقا

إرنست ماخ: توحيد الفيزياء عبر الإدراكات الحسية واستبعاد الميتافيزيقا

"الفيزياء بين الكلاسيكية والكم: من حتمية الأشياء إلى نسبية القوانين"

قوانين البقاء في الفيزياء The Conservation Laws of Physics

من كاسيرر إلى ميكانيكا الكم: تطور مفهوم السببية في الفيزياء والفلسفة

نظرة فلسفية لميكانيكا الكم: هل يمكن فهم الحياة بمفاهيم الفيزياء؟

الطول والزمن في النسبية: التحدي الفيزيائي للفلسفة التقليدية

نسبية الطول بين الفيزياء والفلسفة: أينشتاين في مواجهة فالين