لنعتبر جُسيمًا كتلته m وكان موضعه 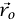 وسرعته  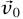عند لحظة زمنية معينة t₀، وعند لحظة أخرى بعدها t_f يكون موضعه  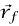وسرعته 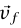. ليكن W هو الشغل الكلي المبذول على الجسيم ليتحرك من  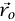إلى 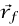. تؤكد نظرية الشغل والطاقة على أن:

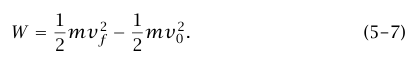
الكمية mv²(2/1) تسمى طاقة الحركة للجسيم؛ وبهذا يمكن صياغة نظرية الشغل والحركة على النحو التالي:

الشغل المبذول على جسيم خلال أي فترة زمنية يساوي التغير في طاقة حركته. (حيث يعرف التغير في كمية ما بالقيمة النهائية للكمية مطروحةً منها قيمتها الابتدائية.) لإثبات هذه النظرية نبدأ بقانون نيوتن الثاني 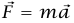 ونأخذ حاصل الضرب القياسي لكلا الجانبين مع متجه السرعة اللحظية 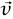، ونحصل على:

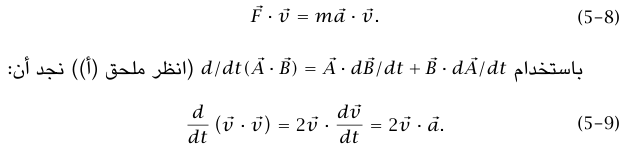
ويكون:

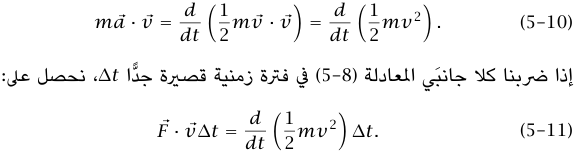
وبما أن 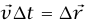؛ حيث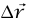 هي الإزاحة التي تحركها الجسيم أثناء الفترة الزمنية tΔ، والجانب الأيسر للمعادلة (11–5) هو الشغل WΔ المبذول على الجسيم أثناء الفترة الزمنية tΔ، الجانب الأيمن للمعادلة (11–5) هو بالضبط التغير الحادث في الكمية mv²(2/1) أثناء الفترة الزمنية tΔ؛ وبناءً على ذلك فإن الشغل المبذول على الجسيم أثناء أي فترة زمنية قصيرة يساوي التغير في طاقة حركته أثناء هذه الفترة الزمنية. بتقسيم الفترة الزمنية من t₀ إلى t_f إلى فترات زمنية قصيرة وعديدة، فإننا نرى أن الشغل الكلي المبذول على الجسيم أثناء هذه الفترة يساوي طاقة الحركة النهائية مطروحةً منها طاقة الحركة الابتدائية؛ مما يثبت صحة المعادلة (7–5). تطبيق نظرية الشغل والطاقة على جسيم يسقط سقوطا حرا يؤدي إلى:

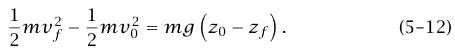
هذه النتيجة تنتج مباشرة من عملنا في الفصل الأول (تذكر أن v_x وv_y ثابتتان أثناء السقوط الحر؛ ولذا فإن v_z هي الوحيدة المتغيرة، لكننا الآن نستطيع أن نبين أن المعادلة (12–5) صحيحة أيضًا في حالات عديدة لا يكون الجسيم فيها ساقطًا بحرية. اعتبر، على سبيل المثال، جُسيمًا ما يتحرك تحت تأثير الجاذبية على سطح أملس بأي شكل. في هذه الحالة، كلٌّ من مقدار عجلة الجسيم واتجاهها سيتغيران عادةً مع الزمن؛ ومن ثم فإن تحليل الحركة بعجلة ثابتة في الفصل الأول غير قابل للتطبيق.

ومع ذلك، فإن نظرية الشغل والطاقة قابلة دائمًا للتطبيق، بشرط أن نأخذ الحذر ومع لحساب الشغل الكلي المبذول على الجسيم بواسطة جميع القوى المؤثرة عليه. نلاحظ أن أي سطح أملس لا يبذل أي قوة موازية له. في هذه الحالة توجد قوتان فقط تؤثران على الجسيم: قوة الجاذبية التثاقلية 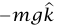 والقوة العمودية  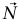التي يبذلها السطح. وكما لاحظنا للتو، أي قوة عمودية على السطح لا تستطيع بذل شغل؛ ومن ثُمَّ فإن  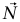لا تبذل شغلًا لأن  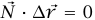وذلك إذا كانت  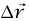إزاحة صغيرة في السطح. القوة الوحيدة التي تبذل شغلًا هي قوة الجاذبية التثاقلية؛ ولهذا فإن المعادلة (12–5) صحيحة.

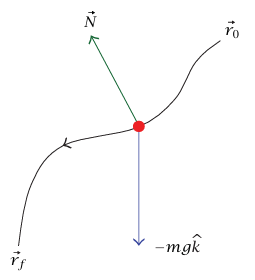
شكل 5–3: الشغل المبذول بواسطة الجاذبية.

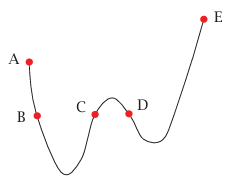
شكل 5–4: جسيم يبدأ من السكون عند A سيكون له نفس مقدار السرعة عند B وC وD ولن يصل أبدًا إلى E.

إذا جعلنا الحالة «النهائية» في المعادلة (12–5) نقطة اختيارية في حركة الجسيم، فإننا نستطيع حذف اللاحقة ”f“ ونكتب:

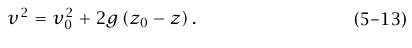
المعادلة (13–5) توضح أن مقدار سرعة الجسيم يعتمد فقط على ارتفاعه z (وعلى القيمتين الابتدائيتين v₀ وz₀)، ولا يعتمد على شكل السطح. إذا بدأ الجسيم من السكون فإنه لن يصل أبدًا إلى ارتفاع أكبر من ارتفاعه الابتدائي؛ لأن المعادلة (13–5) سوف تفضي إلى قيمة سالبة لـ v² إذا كان z₀ < z.

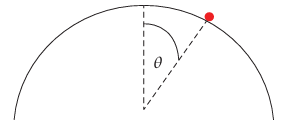
شكل 5–5: جسيم يبدأ من السكون عند قمة نصف كرة وأعطي دفعة متناهية في الصغر في مثال 5–2.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل