Born: 2nd century BC
Died: 2nd century BC

There are only two references to Perseus and these both occur in the writings of Proclus. They give no indication of where he was born or where he lived. His dates can at least be put within certain bounds by the information given, but our knowledge is still almost nil.

The first reference says that Perseus is associated with the discovery of the "spiric" curves in the same way as that of Apollonius is with conics. The second reference is taken from Geminus and says that Perseus wrote an epigram on his discovery (see for example [1]):-

Three curves upon five sections finding, Perseus made offering to the gods...

All that can be deduced with certainty is that Perseus must have lived before Geminus. Less certain, but still very reasonable, is the belief that conic sections must have been developed first so he would then have lived after Euclid wrote in say 300 BC.

The references do not really give enough details to be able to tell what Perseus discovered. We do know what a spiric section is. Proclus defines a spiric surface as being the surface generated by a circle revolving about a straight line called the axis of revolution and always remaining in the same plane as this axis. There are three distinct types of spiric surfaces depending whether the axis of revolution cuts the circle, it is a tangent to the circle, or is outside the circle.

A spiric section is then the curve produced when a plane parallel to the axis of revolution cuts the spiric surface. However, it is now difficult to see what the "three curves upon five sections finding ..." means. Paul Tannery in [3] gives a clever argument based on assuming that Proclus made an error and should have written "three curves in addition to five sections finding ...".

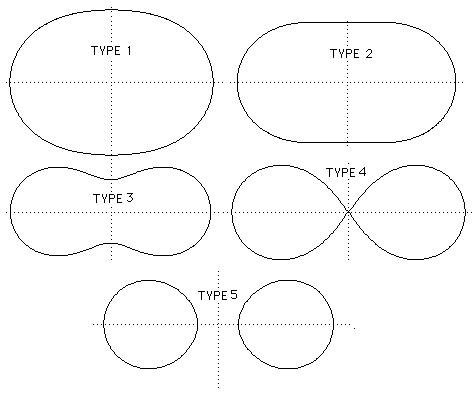The five types of curve are shown in the diagram. The first is the case of an oval, the second is a transition from the first case to the third. The third case is that in which the curve is closed and narrowest in the middle. The fourth case is that of the hippopede, which was studied by Eudoxus. Finally the fifth case consists of two symmetrically positioned closed curves. Proclus gives the three curves of types 1, 3 and 4 only.
 

In [1] Bulmer-Thomas prefers the simpler suggestion that Perseus found five sections but only three of these gave new curves, the other two (types 2 and 5) gave curves which were closely related to the others and not considered new. Another possibility, which is not favoured by historians, is that the three spiric curves were one from each of the three different spiric surfaces.

1. I Bulmer-Thomas, Biography in Dictionary of Scientific Biography (New York 1970-1990). 
   http://www.encyclopedia.com/topic/Perseus.aspx

Books:

1. T L Heath, A history of Greek mathematics I, II (Oxford, 1931).

Articles:

1. P Tannery, Pour l'histoire des lignes et de surfaces courbes dans l'antiquité, Bull. des sciences mathématique et astronomique 8 (1884), 19-30.

مواضيع ذات صلة

Zu Geng

Zu Chongzhi

Zhang Heng

Zenodorus

Zeno of Sidon

Zeno of Elea

Yavanesvara

Xu Yue

Xiahou Yang

Xenocrates of Chalcedon

Thymaridas of Paros

Theon of Smyrna