
ominance
 المؤلف:
Skiena, S
المؤلف:
Skiena, S
 المصدر:
Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, 1990.
المصدر:
Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, 1990.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 5-1-2022
5-1-2022
 1530
1530
ominance
The dominance relation on a set of points in Euclidean 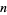 -space is the intersection of the
-space is the intersection of the 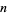 coordinate-wise orderings. A point
coordinate-wise orderings. A point 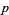 dominates a point
dominates a point 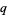 provided that every coordinate of
provided that every coordinate of 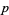 is at least as large as the corresponding coordinate of
is at least as large as the corresponding coordinate of 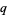 .
.
A partition 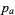 dominates a partition
dominates a partition 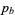 if, for all
if, for all 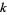 , the sum of the
, the sum of the 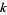 largest parts of
largest parts of 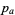 is
is 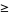 the sum of the
the sum of the 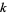 largest parts of
largest parts of 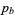 . For example, for
. For example, for 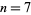 ,
, ![<span style=]() {7}" src="https://mathworld.wolfram.com/images/equations/Dominance/Inline16.gif" style="height:15px; width:17px" /> dominates all other partitions, while
{7}" src="https://mathworld.wolfram.com/images/equations/Dominance/Inline16.gif" style="height:15px; width:17px" /> dominates all other partitions, while ![<span style=]() {1,1,1,1,1,1,1}" src="https://mathworld.wolfram.com/images/equations/Dominance/Inline17.gif" style="height:15px; width:107px" /> is dominated by all others. In contrast,
{1,1,1,1,1,1,1}" src="https://mathworld.wolfram.com/images/equations/Dominance/Inline17.gif" style="height:15px; width:107px" /> is dominated by all others. In contrast, ![<span style=]() {3,1,1,1,1,}" src="https://mathworld.wolfram.com/images/equations/Dominance/Inline18.gif" style="height:15px; width:81px" /> and
{3,1,1,1,1,}" src="https://mathworld.wolfram.com/images/equations/Dominance/Inline18.gif" style="height:15px; width:81px" /> and ![<span style=]() {2,2,2,1}" src="https://mathworld.wolfram.com/images/equations/Dominance/Inline19.gif" style="height:15px; width:62px" /> do not dominate each other (Skiena 1990, p. 52).
{2,2,2,1}" src="https://mathworld.wolfram.com/images/equations/Dominance/Inline19.gif" style="height:15px; width:62px" /> do not dominate each other (Skiena 1990, p. 52).
The dominance orders in 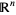 are precisely the partially ordered sets of dimension at most
are precisely the partially ordered sets of dimension at most 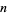 .
.
REFERENCES:
Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, 1990.
Stanton, D. and White, D. Constructive Combinatorics. New York: Springer-Verlag, 1986.
 الاكثر قراءة في نظرية المجموعات
الاكثر قراءة في نظرية المجموعات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


