Maxwell Distribution
المؤلف:
Papoulis, A
المصدر:
Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill
الجزء والصفحة:
...
10-4-2021
2408
Maxwell Distribution
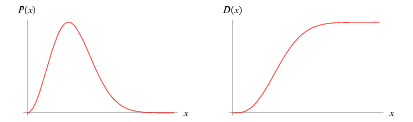
The Maxwell (or Maxwell-Boltzmann) distribution gives the distribution of speeds of molecules in thermal equilibrium as given by statistical mechanics. Defining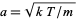 
, where 
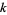is the Boltzmann constant, 
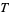is the temperature, 
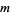is the mass of a molecule, and letting 
denote the speed a molecule, the probability and cumulative distributions over the rang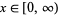e 
are
using the form of Papoulis (1984), where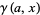 
is an incomplete gamma function and 
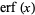is erf. Spiegel (1992) and von Seggern (1993) each use slightly different definitions of the constant 
.
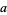It is implemented in the Wolfram Language as MaxwellDistribution[sigma].
The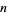 
th raw moment is
 |
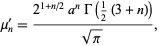(4)
|
giving the first few as
(Papoulis 1984, p. 149).
The mean, variance, skewness, and kurtosis excess are therefore given by
The characteristic function is
![phi(t)=i<span style=]() {atsqrt(2/pi)-e^(-a^2t^2/2)(a^2t^2-1)×[sgn(t)erfi((a|t|)/(sqrt(2)))-i]}, " src="https://mathworld.wolfram.com/images/equations/MaxwellDistribution/NumberedEquation2.gif" style="height:48px; width:384px" /> |
(13)
|
where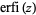 
is the erfi function.
REFERENCES:
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 104 and 148-149, 1984.
Spiegel, M. R. Schaum's Outline of Theory and Problems of Probability and Statistics. New York: McGraw-Hill, p. 119, 1992.
von Seggern, D. CRC Standard Curves and Surfaces. Boca Raton, FL: CRC Press, p. 252, 1993.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
