A random variable is a measurable function from a probability space 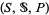 into a measurable space  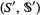known as the state space (Doob 1996). Papoulis (1984, p. 88) gives the slightly different definition of a random variable  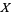as a real function whose domain is the probability space  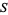and such that:

1. The set {X<=x}" src="https://mathworld.wolfram.com/images/equations/RandomVariable/Inline5.gif" style="height:15px; width:43px" /> is an event for any real number .

2. The probability of the events {X=+infty}" src="https://mathworld.wolfram.com/images/equations/RandomVariable/Inline7.gif" style="height:15px; width:60px" /> and {X=-infty}" src="https://mathworld.wolfram.com/images/equations/RandomVariable/Inline8.gif" style="height:15px; width:60px" /> equals zero.

The abbreviation "r.v." is sometimes used to denote a random variable.

REFERENCES:

Doob, J. L. "The Development of Rigor in Mathematical Probability (1900-1950)." Amer. Math. Monthly 103, 586-595, 1996.

Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, 2000.

Gikhman, I. I. and Skorokhod, A. V. Introduction to the Theory of Random Processes. New York: Dover, 1997.

Papoulis, A. "The Concept of a Random Variable." Ch. 4 in Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 83-115, 1984.