Martingale
المؤلف:
Doob, J. L.
المصدر:
Stochastic Processes. New York: Wiley, 1953.
الجزء والصفحة:
...
21-3-2021
2283
Martingale
A sequence of random variates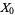 
, 
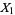, ... with finite means such that the conditional expectation of 
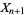given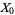 
, 
, 
, ..., 
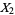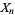is equal to 
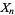, i.e.,
(Feller 1971, p. 210). The term was first used to describe a type of wagering in which the bet is doubled or halved after a loss or win, respectively. The concept of martingales is due to Lévy, and it was developed extensively by Doob.
A one-dimensional random walk with steps equally likely in either direction (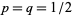
) is an example of a martingale.
REFERENCES:
Doob, J. L. Stochastic Processes. New York: Wiley, 1953.
Feller, W. "Martingales." §6.12 in An Introduction to Probability Theory and Its Applications, Vol. 2, 3rd ed. New York: Wiley, pp. 210-215, 1971.
Lévy, P. Calcul de probabilités. Paris: Gauthier-Villars, 1925.
Lévy, P. Théorie de l'addition des variables aléatoires. Paris: Gauthier-Villars, 1954.
Lévy, P. Processus stochastiques et mouvement Brownien, 2nd ed. Paris: Gauthier-Villars, 1965.
Loève, M. Probability Theory I, 4th ed. New York: Springer-Verlag, 1977.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
