Intensity Function
المؤلف:
Daley, D. J. and Vere-Jones, D.
المصدر:
An Introduction to the Theory of Point Processes Volume I: Elementary Theory and Methods, 2nd ed. New York: Springer, 2003.
الجزء والصفحة:
...
10-3-2021
2298
Intensity Function
There are at least two distinct notions of an intensity function related to the theory of point processes.
In some literature, the intensity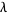 
of a point process 
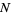is defined to be the quantity
![lambda=lim_(hv0)(Pr<span style=]() {N(0,h]>0})/h " src="https://mathworld.wolfram.com/images/equations/IntensityFunction/NumberedEquation1.gif" style="height:35px; width:142px" /> |
(1)
|
provided it exists. Here,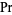 
denotes probability. In particular, it makes sense to talk about point processes having infinite intensity, though when finite, 
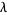allows 
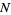to be rewritten so that
![Pr<span style=]() {N(x,x+h]>0}=lambdah+o(h) " src="https://mathworld.wolfram.com/images/equations/IntensityFunction/NumberedEquation2.gif" style="height:15px; width:188px" /> |
(2)
|
as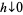 
where here, 
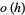denotes little-O notation (Daley and Vere-Jones 2007).
Other authors define the function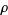 
to be an intensity function of a point process 
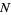provided that 
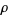is a density of the intensity measure 
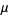associated to 
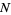relative to Lebesgue measure, i.e.,if for all Borel sets 
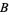in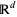 
,
 |
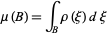(3)
|
where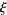 
denotes Lebesgue measure (Pawlas 2008).
REFERENCES:
Daley, D. J. and Vere-Jones, D. An Introduction to the Theory of Point Processes Volume I: Elementary Theory and Methods, 2nd ed. New York: Springer, 2003.
Daley, D. J. and Vere-Jones, D. An Introduction to the Theory of Point Processes Volume II: General Theory and Structure, 2nd ed. New York: Springer, 2007.
Pawlas, Z. "Spatial Modeling and Spatial Statistics." Course Notes. Autumn 2008. https://www.math.ku.dk/~pawlas/rumlig.pdf.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
