
Modular Inverse
 المؤلف:
Sloane, N. J. A
المؤلف:
Sloane, N. J. A
 المصدر:
equence A102057 in "The On-Line Encyclopedia of Integer Sequences."
المصدر:
equence A102057 in "The On-Line Encyclopedia of Integer Sequences."
 الجزء والصفحة:
...
الجزء والصفحة:
...
 10-1-2020
10-1-2020
 1577
1577
Modular Inverse
A modular inverse of an integer 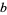 (modulo
(modulo 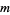 ) is the integer
) is the integer 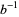 such that
such that
A modular inverse can be computed in the Wolfram Language using PowerMod[b, -1, m].
Every nonzero integer 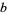 has an inverse (modulo
has an inverse (modulo 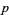 ) for
) for 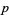 a prime and
a prime and 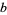 not a multiple of
not a multiple of 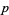 . For example, the modular inverses of 1, 2, 3, and 4 (mod 5) are 1, 3, 2, and 4.
. For example, the modular inverses of 1, 2, 3, and 4 (mod 5) are 1, 3, 2, and 4.
If  is not prime, then not every nonzero integer
is not prime, then not every nonzero integer 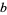 has a modular inverse. In fact, a nonzero integer
has a modular inverse. In fact, a nonzero integer 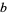 has a modular inverse modulo
has a modular inverse modulo 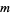 iff
iff 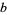 and
and 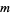 are relatively prime. For example,
are relatively prime. For example, 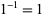 (mod 4) and
(mod 4) and 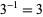 (mod 4), but 2 does not have a modular inverse.
(mod 4), but 2 does not have a modular inverse.
The triangle above (OEIS A102057) gives modular inverses of 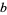 (mod
(mod 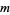 ) for
) for 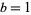 , 2, ...,
, 2, ..., 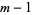 and
and 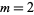 , 3, .... 0 indicates that no modular inverse exists.
, 3, .... 0 indicates that no modular inverse exists.
If 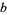 and
and 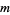 are relatively prime, there exist integers
are relatively prime, there exist integers  and
and 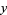 such that
such that 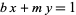 , and such integers may be found using the Euclidean algorithm. Considering this equation modulo
, and such integers may be found using the Euclidean algorithm. Considering this equation modulo 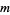 , it follows that
, it follows that 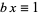 ; i.e.,
; i.e., 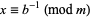 .
.
If 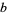 and
and 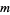 are relatively prime, then Euler's totient theorem states that
are relatively prime, then Euler's totient theorem states that 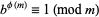 , where
, where 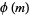 is the totient function. Hence,
is the totient function. Hence, 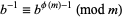 .
.
REFERENCES:
Sloane, N. J. A. Sequence A102057 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


