Jensen,s Theorem
المؤلف:
Cheney, E. W
المصدر:
Introduction to Approximation Theory, 2nd ed. Providence, RI: Amer. Math. Soc., 1999.
الجزء والصفحة:
...
4-3-2019
1669
Jensen's Theorem
There are at least three theorems known as Jensen's theorem.
The first states that, for a fixed vector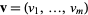 
, the function
is a decreasing function of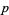 
(Cheney 1999).
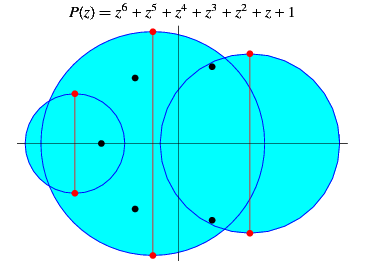
The second states that if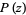 
is a real polynomial not identically constant, then all nonreal zeros of 
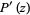lie inside the Jensen disks determined by all pairs of conjugate nonreal zeros of 
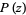(Walsh 1955, 1961; Householder 1970; Trott 2004, p. 22). This theorem is a sharpening of Lucas's root theorem.
The third theorem considers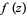 
a function defined and analytic throughout a disk ![<span style=]()
{|z|<=R}" src="http://mathworld.wolfram.com/images/equations/JensensTheorem/Inline7.gif" style="height:14px; width:46px" /> and supposes that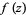 
has no zeros on the bounding circle 
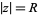, that inside the disk it has zeros 
, 
, ..., 
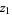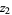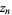(where a zero of order 
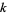is included 
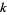times in the list, and that 
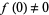. Then
(Edwards 2001, p. 40).
REFERENCES:
Cheney, E. W. Introduction to Approximation Theory, 2nd ed. Providence, RI: Amer. Math. Soc., 1999.
Edwards, H. M. "Jensen's Theorem." §2.2 in Riemann's Zeta Function. New York: Dover, pp. 40-41, 2001.
Householder, A. S. The Numerical Treatment of a Single Nonlinear Equation. New York: McGraw-Hill, 1970.
Rahman, Q. I. and Schmeisser, G. Analytic Theory of Polynomials. Oxford, England: Oxford University Press, 2002.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.
Walsh, J. L. "A Generalization of Jensen's Theorem on the Zeros of the Derivative of a Polynomial." Amer. Math. Monthly 62, 91-93, 1955.
Walsh, J. L. "A New Generalization of Jensen's Theorem on the Zeros of the Derivative of a Polynomial." Amer. Math. Monthly68, 978-983, 1961.
الاكثر قراءة في مواضيع عامة في الجبر
اخر الاخبار
اخبار العتبة العباسية المقدسة
