Fundamental Theorem of Algebra
المؤلف:
Courant, R. and Robbins, H
المصدر:
"The Fundamental Theorem of Algebra." §2.5.4 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press
الجزء والصفحة:
...
19-1-2019
1187
Fundamental Theorem of Algebra
Every polynomial equation having complex coefficients and degree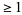 
has at least one complex root. This theorem was first proven by Gauss. It is equivalent to the statement that a polynomial 
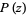of degree 
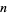has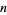 
values 
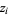(some of them possibly degenerate) for which 
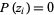. Such values are called polynomial roots. An example of apolynomial with a single root of multiplicity 
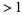is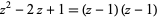 
, which has 
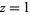as a root of multiplicity 2.
REFERENCES:
Courant, R. and Robbins, H. "The Fundamental Theorem of Algebra." §2.5.4 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 101-103, 1996.
Krantz, S. G. "The Fundamental Theorem of Algebra." §1.1.7 and 3.1.4 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 7 and 32-33, 1999.
Smithies, F. "A Forgotten Paper on the Fundamental Theorem of Algebra." Notes Rec. Roy. Soc. London 54, 333-341, 2000.
الاكثر قراءة في مواضيع عامة في الجبر
اخر الاخبار
اخبار العتبة العباسية المقدسة
