Christoffel Formula
المؤلف:
Szegö, G.
المصدر:
Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc.,
الجزء والصفحة:
pp. 29-30
19-1-2019
1513
Christoffel Formula
Let ![<span style=]()
{p_n(x)}" src="http://mathworld.wolfram.com/images/equations/ChristoffelFormula/Inline1.gif" style="height:14px; width:42px" /> be orthogonal polynomials associated with the distribution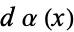 
on the interval ![[a,b]](http://mathworld.wolfram.com/images/equations/ChristoffelFormula/Inline3.gif)
. Also let
(for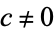 
) be a polynomial of order 
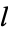which is nonnegative in this interval. Then the orthogonal polynomials ![<span style=]()
{q(x)}" src="http://mathworld.wolfram.com/images/equations/ChristoffelFormula/Inline6.gif" style="height:14px; width:35px" />associated with the distribution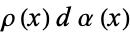 
can be represented in terms of the polynomials 
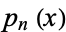as
In the case of a zero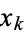 
of multiplicity 
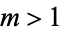, we replace the corresponding rows by the derivatives of order 0, 1, 2, ..., 
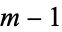of the polynomials 
, ..., 
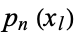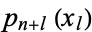at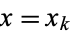 
.
REFERENCES:
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 29-30, 1975.
الاكثر قراءة في مواضيع عامة في الجبر
اخر الاخبار
اخبار العتبة العباسية المقدسة
