Generalized Fourier Integral
المؤلف:
Linton, C. M. and McIver, P
المصدر:
Handbook of Mathematical Techniques for Wave/Structure Interactions. Boca Raton, FL: CRC Press, 2001.
الجزء والصفحة:
...
28-11-2018
921
Generalized Fourier Integral
The so-called generalized Fourier integral is a pair of integrals--a "lower Fourier integral" and an "upper Fourier integral"--which allow certain complex-valued functions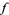 
to be decomposed as the sum of integral-defined functions, each of which resembles the usual Fourier integral associated to 
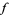and maintains several key properties thereof.
Let 
be a real variable, let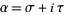 
be a complex variable, and let 
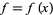be a function for which 
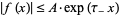as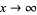 
, for which 
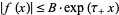as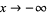 
, and for which 
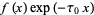has an analytic Fourier integral where here, 
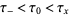are finite real constants. Next, define the upper and lower generalized Fourier integrals 
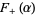and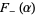 
associated to 
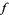, respectively, by
 |
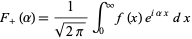(1)
|
and
 |
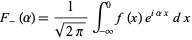(2)
|
on the complex regions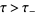 
and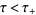 
, respectively. Then, for 
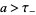and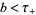 
,
 |
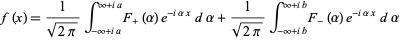(3)
|
where the first integral summand equals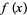 
for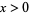 
and is zero for 
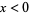while the second integral summand is zero for 
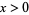and equals 
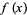for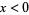 
. The decomposition () is called the generalized Fourier integral corresponding to 
.
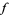Note that some literature defines the upper and lower integrals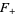 
and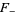 
with multiplicative constants different from 
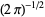, whereby the identity in () may look slightly different.
REFERENCES:
Linton, C. M. and McIver, P. Handbook of Mathematical Techniques for Wave/Structure Interactions. Boca Raton, FL: CRC Press, 2001.
Noble, B. Methods Based on the Wiener-Hopf Technique For the Solution of Partial Differential Equations. Belfast, Northern Ireland: Pergamon Press, 1958.
الاكثر قراءة في التحليل العقدي
اخر الاخبار
اخبار العتبة العباسية المقدسة
