In cylindrical coordinates, the scale factors are 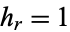, , 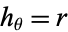, 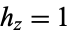so the Laplacian is given by

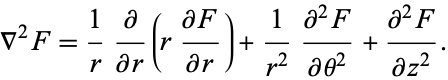(1)

Attempt separation of variables in the Helmholtz differential equation

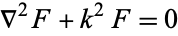(2)

by writing

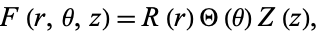(3)

then combining (1) and (2) gives

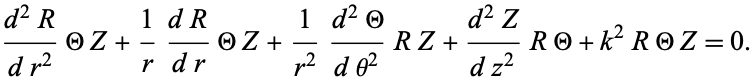(4)

Now multiply by ,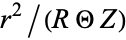

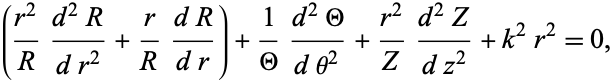(5)

so the equation has been separated. Since the solution must be periodic in 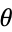 from the definition of the circular cylindrical coordinate system, the solution to the second part of (5) must have a negative separation constant

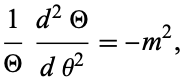(6)

which has a solution

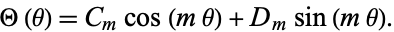(7)

Plugging (7) back into (5) gives

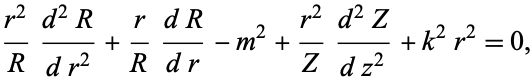(8)

and dividing through by 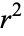 results in

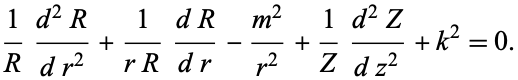(9)

The solution to the second part of (9) must not be sinusoidal at 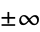 for a physical solution, so the differential equation has a positive separation constant

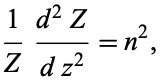(10)

and the solution is

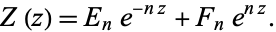(11)

Plugging (11) back into (9) and multiplying through by 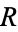 yields

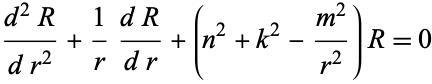(12)

But this is just a modified form of the Bessel differential equation, which has a solution

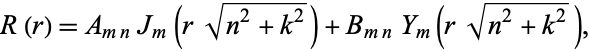(13)

where 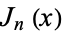 and 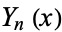 are Bessel functions of the first and second kinds, respectively. The general solution is therefore

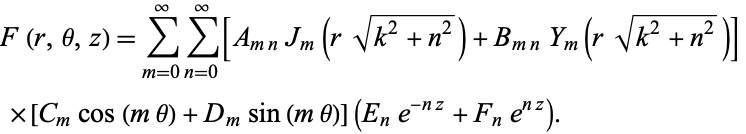(14)

In the notation of Morse and Feshbach (1953), the separation functions are 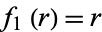, , 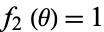, 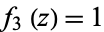so the Stäckel determinant is 1.

The Helmholtz differential equation is also separable in the more general case of 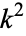 of the form

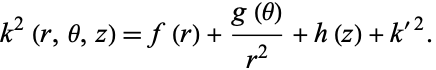(15)a

REFERENCES:

Moon, P. and Spencer, D. E. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed.New York: Springer-Verlag, pp. 15-17, 1988.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 514 and 656-657, 1953.