Lane-Emden Differential Equation
المؤلف:
Chandrasekhar, S
المصدر:
An Introduction to the Study of Stellar Structure. New York: Dover
الجزء والصفحة:
...
22-6-2018
2603
Lane-Emden Differential Equation
A second-order ordinary differential equation arising in the study of stellar interiors, also called the polytropic differential equations. It is given by
 |
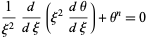(1)
|
 |
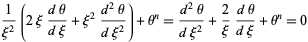(2)
|
(Zwillinger 1997, pp. 124 and 126). It has the boundary conditions
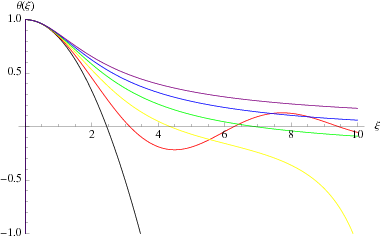
Solutions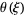 
for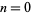 
, 1, 2, 3, and 4 are shown above. The cases 
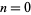, 1, and 5 can be solved analytically (Chandrasekhar 1967, p. 91); the others must be obtained numerically.
For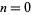 
(
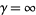), the Lane-Emden differential equation is
 |
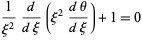(5)
|
(Chandrasekhar 1967, pp. 91-92). Directly solving gives
 |
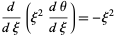(6)
|
 |
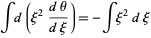(7)
|
 |
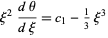(8)
|
 |
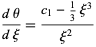(9)
|
 |
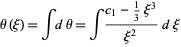(10)
|
 |
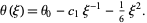(11)
|
The boundary condition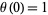 
then gives 
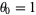and 
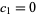, so
 |
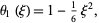(12)
|
and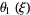 
is parabolic.
For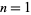 
(
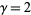), the differential equation becomes
 |
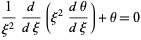(13)
|
 |
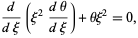(14)
|
which is the spherical Bessel differential equation
![d/(dr)(r^2(dR)/(dr))+[k^2r^2-n(n+1)]R=0](http://mathworld.wolfram.com/images/equations/Lane-EmdenDifferentialEquation/NumberedEquation13.gif) |
(15)
|
with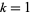 
and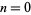 
, so the solution is
 |
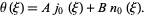(16)
|
Applying the boundary condition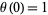 
gives
 |
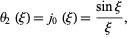(17)
|
where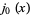 
is a spherical Bessel function of the first kind (Chandrasekhar 1967, p. 92).
For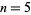 
, make Emden's transformation
which reduces the Lane-Emden equation to
 |
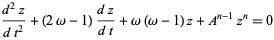(20)
|
(Chandrasekhar 1967, p. 90). After further manipulation (not reproduced here), the equation becomes
 |
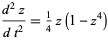(21)
|
and then, finally,
 |
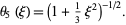(22)
|
REFERENCES:
Chandrasekhar, S. An Introduction to the Study of Stellar Structure. New York: Dover, pp. 84-182, 1967.
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 908, 1980.
Seshadri, R. and Na, T. Y. Group Invariance in Engineering Boundary Value Problems. New York: Springer-Verlag, p. 193, 1985.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, pp. 124 and 126, 1997.
الاكثر قراءة في معادلات تفاضلية
اخر الاخبار
اخبار العتبة العباسية المقدسة
