Homogeneous Ordinary Differential Equation
المؤلف:
Boyce, W. E. and DiPrima, R. C
المصدر:
Elementary Differential Equations and Boundary Value Problems, 8th ed. New York: Wiley
الجزء والصفحة:
pp. 49-50
13-6-2018
1437
Homogeneous Ordinary Differential Equation
A linear ordinary differential equation of order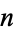 
is said to be homogeneous if it is of the form
 |
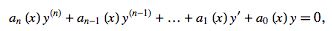(1)
|
where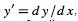 
, i.e., if all the terms are proportional to a derivative of 
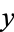(or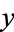 
itself) and there is no term that contains a function of 
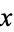alone.
However, there is also another entirely different meaning for a first-order ordinary differential equation. Such an equation is said to be homogeneous if it can be written in the form
 |
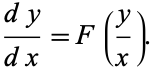(2)
|
Such equations can be solved in closed form by the change of variables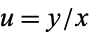 
which transforms the equation into the separable equation
REFERENCES:
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 8th ed. New York: Wiley, pp. 49-50, 2004.
الاكثر قراءة في معادلات تفاضلية
اخر الاخبار
اخبار العتبة العباسية المقدسة
