Critical damping is a special case of damped simple harmonic motion

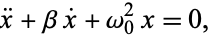(1)

in which

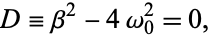(2)

where 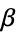 is the damping constant. Therefore

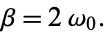(3)

In this case, 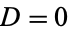 so the solutions of the form  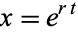satisfy

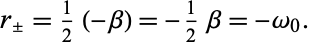(4)

One of the solutions is therefore

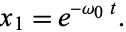(5)

In order to find the other linearly independent solution, we can make use of the identity

(6)

Since we have 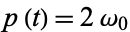,  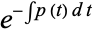simplifies to 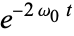. Equation (6) therefore becomes

(7)

The general solution is therefore

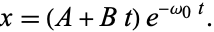(8)

In terms of the constants 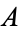 and 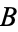, the initial values are

			(9)
			(10)

so

			(11)
			(12)

The above plot shows a critically damped simple harmonic oscillator with 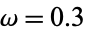,  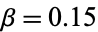for a variety of initial conditions .

For sinusoidally forced simple harmonic motion with critical damping, the equation of motion is

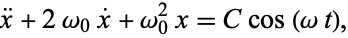(13)

and the Wronskian is

			(14)
			(15)

Plugging this into the equation for the particular solution gives

			(16)
			(17)

Applying the harmonic addition theorem then gives

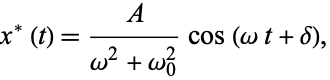(18)

where

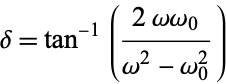(19)

REFERENCES:

Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, p. 528, 1984.